Всё, что есть у меня - Ваше

1. Один человек берет яблоко вместе с корзиной.
2. Иной, пожалуй, начнет вычислять так: 4 кошки в углах, по 3 кошки против каждой — это еще 12 кошек, да на хвосте каждой кошки по кошке, значит, еще 16 кошек. Всего, значит, 32 кошки. Пожалуй, по-своему, он будет и прав. Но еще более прав будет тот, кто сразу сообразит, что в комнате находится всего-навсего четыре кошки. Ни более, ни менее.
3. Если этот вопрос задан быстро и отвечающий не имеет времени на размышление, то часто можно услышать неправильный ответ: по истечении 8 дней. На самом деле последний кусок будет отрезан по истечении 7 дней.
4. Написать это число, а затем повернуть бумажку «вверх ногами» (на 180°). Получится 999.
5. Может, например:
| -3 | = | 5 |
| 6 | -10 |
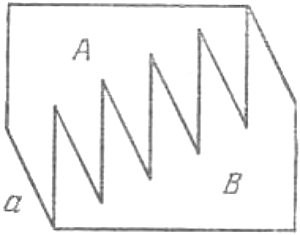
6. Если вы начертите подкову в виде дугообразной линии, как это обычно и делают, то, сколько бы вы ни ломали голову, вам не удастся разрезать ее двумя прямыми более чем на пять частей (рис. a).
|
|
Другое дело, если вы нарисуете подкову имеющей ширину, т. е. так, как она выглядит в действительности. Тогда после нескольких проб вы нападете на верное решение задачи, разрежете подкову двумя прямыми на шесть частей (рис. b).
7. Старик шепнул казакам: «Пересядьте». Те поняли, мигом пересели каждый на лошадь своего противника, и каждый погнал теперь во всю прыть чужую лошадь, на которой он сидел, чтобы собственная его лошадь пришла второй.
1. Четыре спички положены так, как показано на рисунке задачи. Прибавляя к ним еще пять, положенных поперечно, образуем слово сто.

2. Спички прикладываются так, как показано на рисунке. Образуется слово: три.
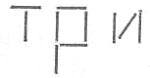
3. См. рисунок.
4. См. рисунок.
5. См. рисунок.
6. См. рисунок.

7. См. рисунок.
8. См. рисунок.
9. См. рисунок.
10. См. рисунок.
11. См. рисунок.
12. См. рисунок.
13. См. рисунок.
14. См. рисунок.

15. См. рисунок.

16. См. рисунок.

17. См. рисунок.

18. См. рисунок.

19. 1) Это можно сделать, например, так, как показано на рисунке.

2) Решения приведены на рисунке.

20. Можно смело поручиться, что мало кому сразу придет в голову решение этой простой задачи. Дело в том, что в данном случае приходится строить из спичек не плоскую фигуру, а фигуру в пространстве.
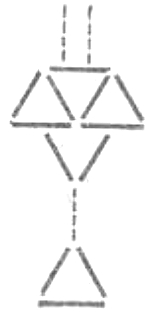
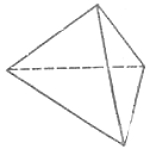
Задачу решите, вглядевшись в рисунок. На нем изображена треугольная пирамида, все грани которой являются равными между собою равносторонними треугольниками. Положите на стол три спички так, чтобы они составили треугольник, затем поставьте остальные три спички, так, чтобы они нижними своими концами упирались в углы лежащего на столе треугольника, а верхними концами соединялись вместе над его серединою, — и вы выполните то, что требуется задачей.
21. Эта на первый взгляд трудная задача решается, однако, легко. Положим на стол спичку А (рисунок),
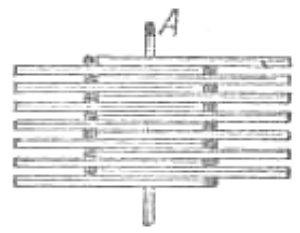
а поперек этой спички положим затем вплотную одну около другой попеременно вправо и влево головками четырнадцать спичек так, чтобы их головки выдавались на 1 - 1,5 сантиметра над А, в то время как противоположные концы опирались бы на стол. Сверху в углубление, образуемое верхними частями спичек, положим шестнадцатую спичку параллельно А. Если поднять теперь спичку А за конец, то, к нашему удивлению, вместе с ней поднимутся и остальные 15 спичек (рисунок).
1. Напрашивающийся ответ «семь», конечно же, неверен. Нужно учитывать как те суда, которые уже плывут в Гавр, так и те, которые еще будут отправляться в путь.
В момент выхода парохода из Гавра в пути, направляясь в Гавр, находится 8 судов компании (одно 128 из них входит в Гавр и одно выходит из Нью-Йорка). Наш пароход встретит все эти 8 судов. Кроме того, в течение его семидневного плавания из Нью-Йорка выйдет еще 7 судов (последнее — в момент прихода парохода в Нью-Йорк). Они также будут встречены пароходом. Итак, правильный ответ — 15 судов.
Представим себе решение задачи нагляднее, с помощью графика. На рисунке нарисованы графики движения пароходов компании, дни отложены по горизонтальным осям.
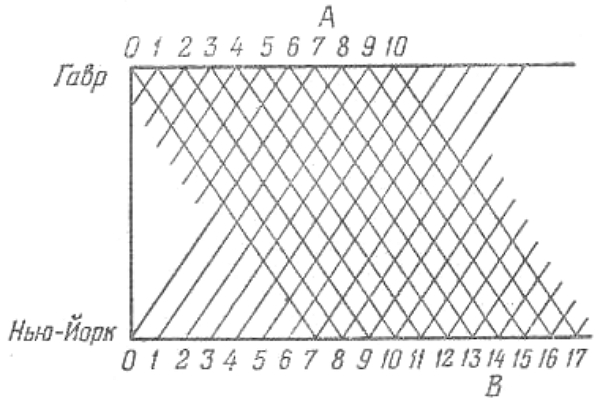
Из рисунка видно, что пароход, график движения которого изображен отрезком АВ, встретит в океане 13 судов, да еще два в момент отправления и прибытия, а всего 15 судов. График показывает, кроме того, что встречи будут происходить ежедневно в полдень и в полночь.
2. Задача сразу решается, если сообразить, что последнему (шестому) покупателю досталось одно целое яблоко. Значит, пятому досталось 2 яблока, четвертому 4, третьему 8 и т. д. Всего же яблок было 1 + 2 + 4 + 8 + 16 + 32 = 63, т. е. крестьянка принесла на рынок 63 яблока.
3. Часто при решении подобных задач рассуждают так: гусеница за сутки, т. е. за 24 ч. всползет на 5 м без 2 м. Значит, всего в сутки она всползет на 3 м. Следовательно, высоты 9 м она достигнет по истечении трех суток, т. е. она будет на этой высоте в среду в 6 ч. утра.
Но такой ответ, очевидно, неверен: в конце вторых суток, т. е. во вторник в 6 ч. утра, гусеница будет на высоте б м; но в этот же день, начиная с шести часов утра, она до 18 ч может всползти еще на 5 м. Следовательно, на высоте 9 м, как легко рассчитать, она окажется во вторник в 13 ч 12 мин. (Естественно, надо считать, что гусеница все время движется равномерно.)
4. Очень часто при решении этой задачи пускаются в разные «тонкие» и сложные выкладки и соображения, не дав себе труда уяснить, что муха, не останавливаясь, летела ровно 3 часа, а следовательно, пролетела 300 километров.
5. Эта задача очень похожа на предыдущую. Ответ не зависит от того, кому из путешественников, первому или второму, принадлежит собака. Второй путешественник догонит первого через 4 ч, и за это время собака пробежит 4 х 15 = 60 км.
6. Всякое число, оканчивающееся на 5, можно представить в виде 10а + 5, где а — число десятков. Тогда
(10а + 5)2 = 100а2 + 2 • 5 • 10а + 25 = 100а2 + 100а + 25 = а • (а + 1) • 100 + 25.
Это равенство показывает, почему к числу а • (а + 1) нужно справа дописать 25, чтобы получить квадрат числа 10а + 5.
Аналогичным приемом можно пользоваться при возведении в квадрат не только двухзначных, но и любых целых чисел, оканчивающихся на 5. В этом случае не всегда легко производить нужные вычисления в уме. Однако он создает большую экономию во времени при умножении на бумаге. Так, например,
10 • 11 = 110, значит, 1052 = 11 025,
12 • 13 = 156, значит, 1252 = 15 625,
123 • 124 = 15 252, значит, 1 2352 = 1 525 225.
7. Так как при перенесении цифры 2 на первое место число удваивается, то предпоследняя цифра его должна быть 4 (2 • 2 = 4), предшествующая ей должна быть 8 (2 • 4 = 8), перед ней б (8 • 2 =16), затем 3 (1 +2 • 6 = 13), затем 7 (1 +2 • 3 = 7) и так далее. Наше число должно начинаться с 1. Поэтому следует остановиться, когда после удвоения цифры и добавления 1 от цифр предыдущего разряда мы получим 1. Искомое число
105 263 157 894 736 842.
Это одно из чисел, удовлетворяющих условию задачи. Все остальные (их бесконечно много) можно получить, продолжая указанный процесс далее. Легко видеть, что каждое из них будет состоять из повторяющейся несколько раз комбинации цифр, уже найденной нами.
8. Легко видеть, что если к искомому числу добавить единицу, то результат будет делиться без остатка на 2, 3, 4, 5 и 6. Наименьшее число с этим свойством есть 60 (наименьшее общее кратное) и все такие числа содержатся в ряду 60, 120, 180, ... Искомое число делится на 7, значит в указанном ряду нужно найти число, дающее при делении на 7 остаток 1. Этому условию отвечает число 120. Итак, число 119 — наименьшее, решающее задачу.
10. Нужно подойти к каждому яблоку и возвратиться обратно к корзине. Значит, число пройденных метров будет равно удвоенной сумме первых ста чисел, или сто раз взятому 101, т. е. 10 100. Это составит почти ровно десять километров. Как видим, способ собирания довольно утомительный!
11. Наибольшее количество ударов, отбиваемых обыкновенными часами, есть 12. Задача сводится к тому, чтобы узнать сумму всех чисел от 1 до 12. А это, мы уже знаем, будет половина двенадцать раз взятых тринадцати. Но в сутках два раза 12 часов, или 24 часа. Значит, часы сделают ровно 12 раз по 13 ударов, т. е. 156 ударов (12 х 13 = 156).
Если же часы отбивают также и получасы, то сколько всего ударов они делают в сутки? Полагаю, что вы без труда ответите на этот вопрос.
13. Нам нужно найти сумму всех нечетных чисел от 1 до 2n - 1 и убедиться, что она равна n2. Это можно сделать различными способами. Мы предпочли геометрический.

Возьмем квадрат из n2 клеток и заштрихуем клетки так, как это сделано на рисунке для n = 6. Квадрат при этом распадается на чередующиеся по цвету участки. Сосчитаем количество клеток в них, начиная с левого верхнего угла. Первый участок состоит из одной клетки, второй — из 3 клеток, третий — из 5 и так далее, последний n-й участок состоит из 2n - 1 клеток. Следовательно, число клеток в квадрате равно
1 + 3 + 5 + 7 + . . . + 2n - 1.
Это убеждает нас, что нужное равенство выполнено всегда. С помощью геометрических представлений можно вычислять и многие другие суммы.
1. Стоит взглянуть на прилагаемый здесь рисунок, чтобы понять, как решается задача.
Что касается математического доказательства возможности подобной переправы, то оно следует из неравенства 2 √2¯ < 3 и делается очевидным, если принять ширину рва равной трем каким-либо единицам.
2. Дети переехали реку. Один из мальчиков остался на берегу, а другой пригнал лодку к солдатам и вылез. Тогда сел солдат и переправился на другой берег. Мальчик, оставшийся там, пригнал обратно лодку к солдатам, взял своего товарища, отвез на другой берег и снова доставил лодку обратно, после чего вылез, а в нее сел другой солдат и переправился. Таким образом — после каждых двух перегонов лодки через реку и обратно — переправлялся один солдат. Так повторялось столько раз, сколько было солдат.
3. Ясно, что приходится начать с козы. Крестьянин, перевезя козу, возвращается и берет волка, которого перевозит на другой берег, где его и оставляет, но зато берет и везет обратно на первый берег козу. Здесь он оставляет ее и перевозит к волку капусту. Вслед затем, возвратившись, он перевозит козу, и переправа оканчивается благополучно.
4. Задача имеет почтенную давность. Обозначим большими буквами А, Б, В рыцарей, а их оруженосцев соответственно малыми а, б, в. Имеем:
| Первый берег | Второй берег | ||||
| А | Б | В | • | • | • |
| а | б | в | • | • | • |
I. Сначала отправляются два оруженосца:
| А | Б | В | • | • | • |
| • | • | в | а | б | • |
II. Возвращается один из оруженосцев и перевозит третьего:
| А | Б | В | • | • | • |
| • | • | • | а | б | в |
III. Возвращается один из оруженосцев и остается со своим рыцарем. Два других рыцаря отправляются к своим оруженосцам:
| • | • | В | А | Б | • |
| • | • | в | а | б | • |
IV. Один из рыцарей возвращается со своим оруженосцем, оставляет его и забирает с собой рыцаря:
| • | • | • | А | Б | В |
| • | б | в | а | • | • |
V. Оруженосец а переезжает и забирает одного из оставшихся оруженосцев:
| • | • | • | А | Б | В |
| • | • | в | а | б | • |
VI. Рыцарь забирает своего оруженосца:
| • | • | • | А | Б | В |
| • | • | • | а | б | в |
5. Четыре рыцаря со своими оруженосцами не смогут переправиться с первого берега на второй, соблюдая условия задачи. Чтобы объяснить это, предположим, что переправа возможна, и перенумеруем, начиная с первого, все рейсы, которые совершит лодка. Тогда после нечетных рейсов она будет находиться на втором берегу, а после четных — на первом. Обозначим через 2k + 1 наименьший номер нечетного рейса, в результате которого на втором берегу окажется более двух рыцарей. Рейс с номером 2k + 1 может доставить на второй берег не более двух человек, поэтому после рейса 2k - 1 на втором берегу должен находиться по крайней мере один рыцарь. Мы видим, что после рейса 2k - 1 на втором берегу могут находиться или один, или два рыцаря.
В первом случае обозначим рыцарей, оставшихся па первом берегу, через А, Б, В, а рыцаря на втором берегу — через Г. Если соответствующих оруженосцев обозначить а, 6, в, г, то с соблюдением условий задачи возможно единственное распределение оруженосцев. Итак, в первом случае после рейса с номером 2k - 1 мы получим такую картину:
| Первый берег | Второй берег | ||||
| А | Б | В | Г | ||
| а | б | в | г | ||
Кто же отправится в лодке рейсом 2k? Рыцарь Г уплыть им не может, ведь тогда после рейса 2k + 1 на втором берегу будет не более двух рыцарей. Значит, рейсом 2k поплывет один оруженосец г, но тогда на первом берегу он окажется в обществе чужих рыцарей, что противоречит условию задачи. В рейс 2k плыть некому. Это означает, что первый случай невозможен.
Во втором случае обозначим рыцарей на первом берегу через А, Б и переправившихся рыцарей через В, Г. Тогда после рейса 2k - 1 имеем:
| Первый берег | Второй берег | ||||
| А | Б | В | Г | ||
| а | б | в | г | ||
Кто же в этом случае отправится рейсом 2k? Ни один из рыцарей В, Г уплыть не может, так как тогда рейсом 2k + 1 с первого берега должны плыть два рыцаря и один из оруженосцев а или б остается без охраны. Но ни один из оруженосцев в, г не может плыть рейсом 2k без своего рыцаря, ведь на первом берегу находятся А, Б. Опять в рейс 2k плыть некому.
Итак, мы установили, что с соблюдением условий задачи на второй берег не может переправиться более двух рыцарей.
6. Обозначим рыцарей буквами А, Б, В, Г, а их оруженосцев а, б, в, г соответственно.
| Первый берег | Второй берег | ||||||
| А | Б | В | Г | • | • | • | • |
| а | б | в | г | • | • | • | • |
I. Переправляются оруженосцы б, в, г:
| Первый берег | Второй берег | ||||||
| А | Б | В | Г | • | • | • | • |
| а | • | • | • | • | б | в | г |
II. Оруженосец б возвращается, а рыцари В, Г переправляются на другую сторону:
| Первый берег | Второй берег | ||||||
| А | Б | • | • | • | • | В | Г |
| а | б | • | • | • | • | в | г |
III. Рыцарь В и его оруженосец переезжают назад. Затем рыцари А, Б, В переправляются на второй берег:
| Первый берег | Второй берег | ||||||
| • | • | • | • | А | Б | В | Г |
| а | б | в | • | • | • | • | г |
IV. Оруженосец г забирает оруженосцев б, в:
| Первый берег | Второй берег | ||||||
| • | • | • | • | А | Б | В | Г |
| а | • | • | • | • | б | в | г |
V. Один из оруженосцев перевозит последнего оруженосца а:
| Первый берег | Второй берег | ||||||
| • | • | • | • | А | Б | В | Г |
| • | • | • | • | а | б | в | г |
7. Будем пользоваться обозначениями предыдущих задач:
| Первый берег | Остров | Второй берег | ||||||
| А | Б | В | Г | • | • | • | • | |
| а | б | в | г | • | • | • | • | |
I. Рыцарь Г перевозит своего оруженосца на остров и возвращается назад:
| Первый берег | Остров | Второй берег | ||||||
| А | Б | В | Г | • | • | • | • | |
| а | б | в | • | г | • | • | • | • |
II. Рыцарь В перевозит своего оруженосца на второй берег и возвращается назад:
| Первый берег | Остров | Второй берег | ||||||
| А | Б | В | Г | • | • | • | • | |
| а | б | • | • | г | • | • | в | • |
III. Рыцарь В перевозит на остров рыцаря Г, заезжает за своим оруженосцем и возвращается с ним на первый берег:
| Первый берег | Остров | Второй берег | ||||||
| А | Б | В | • | Г | • | • | • | • |
| а | б | в | • | г | • | • | • | • |
IV. Рыцари А, Б, В и их оруженосцы переправляются, не заезжая на остров (см. задачу "Переправа трёх рыцарей с оруженосцами"):
| Первый берег | Остров | Второй берег | ||||||
| • | • | • | • | Г | А | Б | В | • |
| • | • | • | • | г | а | б | в | • |
V. Рыцарь А со своим оруженосцем переезжает на остров, оставляет там оруженосца и перевозит на второй берег рыцаря Г:
| Первый берег | Остров | Второй берег | ||||||
| • | • | • | • | А | Б | В | Г | |
| • | • | • | • | а, г | • | б | в | • |
VI. Оруженосец в перевозит сначала а, затем г:
| Первый берег | Остров | Второй берег | ||||||
| • | • | • | • | А | Б | В | Г | |
| • | • | • | • | а | б | в | г | |
8. Железнодорожный путь у станции имеет такой вид, как показано на рисунке.
По главному пути в направлении, обозначенном стрелкой, идут впереди поезд Б, а за ним поезд А, который надо пропустить вперед, пользуясь боковою веткой, где может поместиться лишь часть вагонов.
Поезд А нагнал поезд Б и должен пройти дальше. Как же быть? А вот как.

Поезд Б идет по главному пути и переходит весь за начало боковой ветки. Затем поезд Б идет задним ходом на это ответвление и оставляет там столько вагонов, сколько умещается, а остальная часть поезда Б вместе с паровозом уходит опять вперед, за начало ветки. Затем пропускают поезд А и, как только он весь пройдет за начало ветки, к последнему его вагону прицепляют оставшиеся на ветке вагоны поезда Б, а поезд А сводит эту часть поезда Б с ветки вперед. Затем поезд А пускают назад, влево от начала ветки, и оставляют там вагоны от поезда Б. В это время другая часть поезда Б (с паровозом) идет задним ходом и становится на ветку, открывая свободный путь для поезда А. Он мчится дальше, а паровоз поезда Б с несколькими передними вагонами опять выходит на главный путь, прицепляет стоящую влево от начала ветки часть своего поезда и следует за поездом А.
9. Положение судов и канал с заливом изображены на рисунке.

Пароходы Б и В отходят назад (вправо), А входит в залив; Г, Д и Е проходят по каналу мимо А; тогда А выходит из залива и идет своей дорогой (влево), Е, Д и Г отступают на прежнее место (налево); тогда с Б повторяется все, что делалось с А. Таким же образом проходит и В, и пароходы плывут своей дорогой.
1. Если мы из 5 данных пряников 3 разрежем пополам, то получим 6 равных кусков, каждый из которых и отдадим мальчикам. Затем 2 оставшихся пряника разрежем каждый на 3 равных части и получим опять 6 равных кусков, которые и отдадим мальчикам. Таким образом, задача решена, причем ни одного пряника не пришлось разрезать на 6 частей.
2. И Никита и Павел делают неправильный расчет. 11 лепешек разделены на троих поровну, значит, каждый съел 11/3 лепешки.
У Павла было 7 лепешек, он съел 11/3 лепешки, следовательно, охотнику отдал 10/3 лепешки.
Никита из четырех своих лепешек съел тоже 11/3 лепешки, следовательно, охотнику отдал 1/3 (одну треть) лепешки.
Охотник съел 11/3 лепешки и заплатил за них 11 копеек, значит, за каждую треть лепешки он дал по копейке. У Павла он взял 10 третей, у Никиты — одну треть; следовательно, Павел должен взять себе гривенник, а Никита — копейку.
3. Иван предложил крестьянам делить зерно так:
— Я рассыпаю зерно на три кучи на мой взгляд поровну, и отхожу в сторону. Мне подойдет любая из куч. Пусть затем Петр укажет наименьшую по его мнению кучу зерна. Если Николай также посчитает, что зерна в этой куче меньше трети, то отдайте ее мне, а остаток зерна делите между собой известным уже способом. Если же Николай решит, что в указанной куче не меньше трети зерна, пусть возьмет ее себе. Петр возьмет наибольшую по его мнению кучу, а оставшаяся достанется мне.
Крестьяне последовали предложению Ивана, разделили зерно и довольные разошлись.
4. Предполагается, конечно, что все бочонки — полные, полные наполовину и пустые — равны между собою. Ясно, что каждый должен получить по семи бочонков. Подсчитаем теперь, сколько же кваса должно прийтись на долю каждого. Есть 7 бочонков полных и семь пустых. Если бы можно было от каждого полного бочонка отлить половину в пустой, то получилось бы 14 наполовину полных бочонков; прибавляя к ним еще 7 имеющихся наполовину полных, мы получили бы всего 21 полный наполовину бочонок. Значит, на долю каждого должно прийтись по 7 наполовину 138 полных бочонков вина. Сообразив это, получаем, что, не переливая кваса, можно поделить все поровну так:
| Полные бочки | Полные наполовину бочонки | Пустые бочонки | |
| Первый человек | 2 | 3 | 2 |
| Второй человек | 2 | 3 | 2 |
| Третий человек | 3 | 1 | 3 |
А вот и другое решение:
| Полные бочки | Полные наполовину бочонки | Пустые бочонки | |
| Первый человек | 3 | 1 | 3 |
| Второй человек | 3 | 1 | 3 |
| Третий человек | 1 | 5 | 1 |
5. Задача эта имеет два решения, и решения эти состоят, очевидно, в том, что из полного восьмиведерного бочонка нужно отливать квас в пустые бочонки, из этих последних переливать опять и т. д. Дадим эти решения в виде двух таблиц, которые показывают, сколько в каждом бочонке остается кваса после каждого переливания.
Решение 1
| Большой |
Бочонки 5-вёдерные |
3-вёдерные | |
| До переливания | 8 | 0 | 0 |
| После 1-го переливания | 3 | 5 | 0 |
| » 2-го » | 3 | 2 | 3 |
| » 3-го » | 6 | 2 | 0 |
| » 4-го » | 6 | 0 | 2 |
| » 5-го » | 1 | 5 | 2 |
| » 6-го » | 1 | 4 | 3 |
| » 7-го » |
4 |
4 |
0 |
Решение 2
| Большой |
Бочонки 5-вёдерные |
3-вёдерные | |
| До переливания | 8 | 0 | 0 |
| После 1-го переливания | 5 | 0 | 3 |
| » 2-го » | 5 | 3 | 0 |
| » 3-го » | 2 | 3 | 3 |
| » 4-го » | 2 | 5 | 1 |
| » 5-го » | 7 | 0 | 1 |
| » 6-го » | 7 | 1 | 0 |
| » 7-го » | 4 | 1 | 3 |
| » 8-го » |
4 |
4 |
0 |
6.
| Решение 1 | Решение 2 | |||||
| Большой | 11-вёдерн. | 6-вёдерн. | Большой | 11-вёдерн. | 6-вёдерн. | |
| 16 | 0 | 0 | 16 | 0 | 0 | |
| 10 | 0 | 6 | 10 | 0 | 6 | |
| 0 | 10 | 6 | 10 | 6 | 0 | |
| 6 | 10 | 0 | 4 | 6 | 6 | |
| 6 | 4 | 6 | 4 | 11 | 1 | |
| 12 | 4 | 0 | 15 | 0 | 1 | |
| 12 | 0 | 4 | 15 | 1 | 0 | |
| 1 | 11 | 4 | 9 | 1 | 6 | |
| 1 | 9 | 6 | 9 | 7 | 0 | |
| 7 | 9 | 0 | 3 | 7 | 6 | |
| 7 | 3 | 6 | 3 | 11 | 2 | |
| 13 | 3 | 0 | 14 | 0 | 2 | |
| 13 | 0 | 3 | 14 | 2 | 0 | |
| 2 | 11 | 3 | 8 | 2 | 6 | |
| 2 | 8 | 6 | 8 | 8 | 0 | |
| 8 | 8 | 0 | ||||
7.
| Решение 1 | Решение 2 | |||||
| 6-вёдерн. | 3-вёдерн. | 7-вёдерн. | 6-вёдерн. | 3-вёдерн. | 7-вёдерн. | |
| 4 | 0 | 6 | 4 | 0 | 6 | |
| 1 | 3 | 6 | 4 | 3 | 3 | |
| 1 | 2 | 7 | 6 | 1 | 3 | |
| 6 | 2 | 2 | 2 | 1 | 7 | |
| 5 | 3 | 2 | 2 | 3 | 5 | |
| 5 | 0 | 5 | 5 | 0 | 5 | |
Легко сформулировать множество подобных задач. Но выписанные таблицы не дают ответа на вопрос: каким же правилом руководствоваться для нахождения решения? С целью найти такое правило давайте представим себе задачу иначе — геометрически. Для определенности рассмотрим эту задачу.
Обозначим через х и у количество жидкости, содержащейся после какого-либо переливания соответственно в первом и втором бочонках. При переливании общее количество жидкости не изменяется, т. е. все время остается равным 4 + 6 = 10 ведрам. Поэтому в третьем бочонке будет находиться 10 - х - у ведер жидкости. Количество жидкости, содержащейся в бочонке, не может быть больше объема бочонка. Мы видим, что числа х и у удовлетворяют таким условиям:
|
{
|
0 ≤ х ≤ 6 |
|
{
|
0 ≤ х ≤ 6 |
| 0 ≤ y ≤ 3 |
или |
0 ≤ y ≤ 3 | ||
| 0 ≤ 10 - х - y ≤ 7 |
|
3 ≤ х + y ≤ 10 |
Для дальнейшего удобно воспользоваться листом клетчатой бумаги. Возьмем такой лист, выберем на нем некоторую точку и проведем через нее две перпендикулярные прямые по линиям нанесенной на бумаге решетки. Одну назовем осью X , другую — осью Y. Каждой паре чисел х, у мы сможем тогда поставить в соответствие некоторую точку на листе бумаги — точку с координатами х, у. Нарисуем на плоскости все точки, координаты которых удовлетворяют написанным выше неравенствам. На рисунке это множество — внутренняя часть четырехугольника PQRS — заштриховано. Начальному распределению жидкости соответствует на этом рис. 1 точка А (х = 4, у = 0). Распределению, которое мы хотим получить, — точка В (х = 5, у = 0, при этом в третьем бочонке будет 5 ведер).
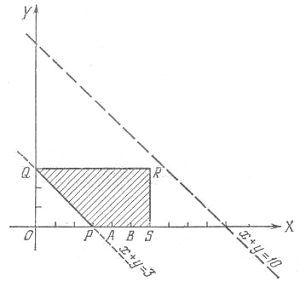
Рис. 1
Последовательность переливаний, ведущая от распределения А к распределению В, представится на этом рисунке в виде некоторой последовательности точек. Или, если мы соединим отрезком прямой линии каждые две последовательные точки, в виде ломаной с началом в точке А и кондом в точке В.
Попробуем выяснить, каким же условиям должны удовлетворять вершины этой ломаной и ее звенья.
Переливание заканчивается, когда наполнится тот бочонок, в который мы льем жидкость, или станет пустым бочонок, из которого мы жидкость выливаем. Это означает, что после каждого переливания обязательно найдется хотя бы один пустой или хотя бы один полный бочонок. Где же на четырехугольнике PQRS будут располагаться соответствующие точки? Если полон первый бочонок (х = 6), то точка лежит на отрезке RS; если первый бочонок пуст (x = 0), то должны быть полными второй и третий бочонки (3 + 7 = 10). Имеется единственная точка с такими условиями точка Q. Распределениям, при которых пуст второй бочонок (у = 0), соответствуют точки отрезка PS, а если второй бочонок полон (у = 3) — точки отрезка QR. Наконец, третий бочонок пустым быть не может, в первые два бочонка 10 ведер не вместятся, а если он полон, то в первых двух должно содержаться 10 — 7 = 3 ведра (х + y = 3). Соответствующие точки лежат на отрезке PQ. В любом случае точки лежат на границе четырехугольника PQRS. Итак, мы установили, что вершины нашей ломаной должны располагаться на границе четырехугольника PQRS.
Заметим теперь, что при каждом переливании содержимое одного бочонка остается неизменным, ведь каждое переливание затрагивает только два бочонка. Если не изменяется содержимое первого бочонка (х постоянно), то отрезок, соединяющий точки, соответствующие распределениям до и после переливания, параллелен оси У (у начала и конца отрезка координата х имеет одно и то же значение). Если при переливании не меняется содержимое второго бочонка, то соответствующее звено ломаной параллельно оси X (у постоянно). Наконец, если в переливании не участвует третий бочонок, то сохраняется общее количество жидкости в первых двух бочонках. Иными словами, в концах отрезка сумма х + у принимает одно и то же значение. Это означает, что звено ломаной параллельно отрезку PQ. Итак, каждое звено ломаной перпендикулярно оси ОХ, или оси ОУ, или биссектрисе угла между этими осями.
Чтобы проверить себя, представим, что некоторое звено ломаной расположено на границе многоугольника PQRS, например на отрезке PQ. Что это означает? Звено образует равные углы с осями X, У, поэтому в переливании не участвует третий бочонок. Кроме того, этот бочонок полон. В первых двух бочонках вместе содержится х + у = 3 ведра жидкости, так что переливание закончится, если станет пустым первый бочонок (х = 0, точка Q) или второй бочонок (у = 0, точка Р). Точно так же можно рассуждать и для других сторон многоугольника PQRS. Мы выяснили, что если некоторое звено ломаной лежит на границе PQRS, то его конец обязательно совпадает с одной из точек Р, Q, R или S.
Наша задача на геометрическом языке выглядит теперь так: соединить точку А с точкой В ломаной, все вершины которой лежат на границе многоугольника, а звенья параллельны осям Х, Y или образуют равные углы с осями. При этом, если звено лежит на стороне многоугольника, то его конец должен совпадать с одной из вершин.
В таком виде задача становится нагляднее, и требуемые ломаные без труда находятся (рис. 2, 3).
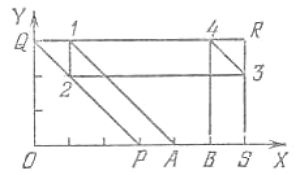
|
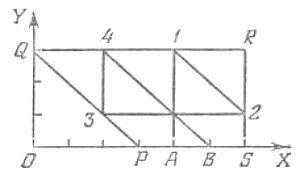 |
|
| рис. 2 | рис. 3 |
На клетчатой бумаге проведение ломаных не составляет никакого труда, так как все звенья проходят через узлы решетки, а вершины совпадают с узлами. Ломаные, представленные на рис. 2, 3, соответствуют первому и второму решениям, в чем легко убедиться. В других задачах роль четырехугольника PQRS могут играть другие многоугольники: параллелограмм (задача "Делёж между двумя"), пятиугольник (задача "Делёж пополам"). Могут встретиться шестиугольники, причем 6 — это максимальное возможное число сторон. Формулировка задачи при этом остается той же самой, изменятся многоугольник и положения точек А, В.
Геометрическое представление задачи и ее решения наглядно, однако выполнение всех построений отнимает лишнее время, требует бумаги и карандаша. Попробуем на основе геометрических соображений дать рекомендации, как в любой подобной задаче найти требуемый способ (если он существует), не прибегая к построениям.
Вершины многоугольника соответствуют распределениям жидкости, при которых сразу два бочонка находятся в граничном состоянии (оба пусты; оба полны; один пуст, другой полон).
I. Прежде всего нужно добиться с помощью переливаний, чтобы по крайней мере два бочонка находились в граничном состоянии.
Геометрически это соответствует тому, что мы строим ломаную, начинающуюся в точке А и кончающуюся в какой-либо вершине многоугольника.
II. Следует обойти все вершины многоугольника, переливая на каждом шаге жидкость из бочонка, который не участвовал в предыдущем переливании, и не изменяя содержимого одного из бочонков, находящихся в граничном состоянии.
Геометрически последовательное применение правила II означает переход от вершины многоугольника к соседней с ним вершине и так далее. Вершин не более шести, поэтому, применяя правило II не более шести раз, мы вернемся к распределению, которое нам ранее уже встречалось.
Если, применяя I, мы не попали в В и если В отлично от вершин многоугольника (применение II не дает нам В), то далее нужно поступать следующим образом.
III. Отправляясь от точки А, а также от распределений, соответствующих каждой вершине многоугольника, совершать переливания, не приводящие к ранее встречавшимся распределениям, пока это будет возможно сделать или встретится распределение В. При этом, как легко видеть, в переливании должны участвовать бочонок, находящийся в граничном состоянии, и бочонок, не участвовавший в предыдущем переливании.
Из геометрических соображений следует, что если это можно сделать, то единственным способом (из точки А иногда можно провести две ломаные, как в рассмотренной задаче). Если применение правила III не приведет к распределению В, то, значит, переливаниями из А в В перейти невозможно.
1. Задача разрешается очень легко, если только решение ее начать с конца, приняв во внимание, что после третьего перехода у крестьянина оказалось ровно 24 коп., которые он должен был отдать.
В самом деле, если после последнего перехода у крестьянина оказалось ровно 24 коп., то, значит, перед этим переходом у него было 12 коп. Но эти 12 коп., получилось после того, как он отдал 24 коп., значит, всего денег у него было 36 коп. Следовательно, второй переход он начал с 18 коп., а эти 18 коп. получились у него после того, как он в первый раз перешел мост и отдал 24 коп. Значит, всего после первого перехода у него было денег 18 да 24 коп., т. е. 42 коп. Отсюда ясно, что перед тем, как первый раз вступить на мост, крестьянин имел в кармане 21 коп. собственных денег.
Прогадал крестьянин! Видно, что на чужой совет всегда надо еще свой ум иметь.
2. Третий крестьянин оставил для товарищей 8 картофелин, т. е. каждому по 4 штуки. Значит, и сам он съел 4 картофелины. После этого легко сообразить, что второй крестьянин оставил своим товарищам 12 картофелин, по 6 на каждого, значит, и сам съел 6 штук. Отсюда следует, что первый крестьянин оставил товарищам 18 картофелин, по 9 штук на каждого, значит, и сам съел 9 штук.
Итак, хозяйка подала на стол 27 картофелин, и на долю каждого поэтому приходилось по 9 картофелин. Но первый крестьянин всю свою долю съел. Следовательно, из восьми оставшихся картофелин приходится на долю второго 3, а на долю третьего 5 штук.
3. Задача старинная и многим известная.
Ясно, что овец больше у первого пастуха, у Ивана. Но на сколько у него больше, чем у Петра?
Если Иван отдаст одну овцу не Петру, а кому-либо другому, то станет ли у обоих пастухов овец 145 поровну? Нет, потому что поровну у них было бы только в том случае, если бы эту овцу получил Петр... Значит, если Иван отдаст одну овцу не Петру, а третьему лицу, то у него все-таки будет больше овец, чем у Петра, но на сколько больше? Ясно, что на одну овцу, потому что если прибавить теперь к стаду Петра одну овцу, то у обоих станет поровну. Отсюда следует, что пока Иван не отдаст никому ни одной своей овцы, то у него в стаде на две овцы больше, чем у Петра.
Теперь примемся за второго пастуха, за Петра. У него, как мы нашли, на две овцы меньше, чем у Ивана. Значит, если Петр отдаст, скажем, одну свою овцу не Ивану, а кому-либо иному, то тогда у Ивана будет на три овцы больше, чем у Петра. Но пусть эту овцу получит именно Иван, а не третье лицо. Ясно, что тогда у него будет на четыре овцы больше, чем осталось у Петра.
Но задача говорит, что у Ивана в этом случае будет ровно вдвое больше овец, чем у Петра. Стало быть, четыре и есть именно то число овец, которое останется у Петра, если он отдаст одну овцу Ивану, у которого получится восемь овец. А до предполагаемой отдачи, значит, у Ивана было 7, а у Петра 5 овец.
4. Недоумение крестьянок разрешается очень быстро, если сообразим, что, сложив свои яблоки вместе и начав их продавать сообща, они, сами того не замечая, продавали их уже по другой цене, чем раньше.
Возьмем, для примера, двух последних крестьянок и рассмотрим, что они, в сущности, сделали.
Пока первая и вторая думали продавать свои яблоки отдельно, цена одного яблока у первой была полкопейки, а у второй — треть копейки. Когда же они сложились и начали продавать каждые пять яблок по 2 коп., то цена каждого яблока стала уже 2/5 коп.
Значит, первая крестьянка все свои яблоки продала не по полкопейки за штуку, а по 2/5 коп. и на каждом яблоке теряла по 1/10 коп.
[1/2 - 2/5 = (5 - 4) : 10 = 1/10],
а на всех тридцати яблоках она потеряла 3 коп.
Вторая же крестьянка, наоборот, вошедши в компанию, выигрывала на каждом яблоке по 1/15 коп.
[2/5 - 1/3 = (6 - 5) : 15 = 1/15],
а на всех тридцати яблоках выиграла, значит, 2 коп.
Первая потеряла 3 коп., а вторая выиграла только 2 коп. В общем, все-таки копейка потеряна.
Путем подобных же рассуждений легко узнать, почему у первых двух крестьянок оказалась «лишняя» копейка.
5. Крестьяне не умели правильно складывать дроби. В самом деле, сложите все части, на которые крестьяне хотели поделить находку:
1/3 + 1/4 + 1/5 + 1/6 = 57/60.
Значит, они все вместе хотели получить меньше, чем нашли (нашли они 60/60). Найденные деньги вместе с деньгами верхового были разделены на 60 частей; из них 57/60 отданы крестьянам, а 3/60, или 1/20, остались у верхового. Но мы знаем, что у верхового осталось 3 руб. Значит, 1/20 всех денег составляют 3 рубля; следовательно, всех денег было 3 х 20 = 60 руб. Карп получил из этих денег 1/4 часть, т. е. 15 руб.; но, если бы верховой не приложил своих денег, Карп должен был бы получить на 25 коп. меньше, т. е.
15 руб. - 25 коп. = 14 руб. 75 коп.:
такова 1/4 часть найденных денег. Отсюда заключаем, что найдено было
14 руб. 75 коп. х 4 = 59 руб.
С деньгами верхового стало 60 руб.; значит, верховой действительно приложил 1 рубль. Приложил он рубль, а увез 3 рубля: 2 рубля выгадал себе за умный дележ.
Какие же деньги были найдены в кошельке?
Пять бумажек по 10 руб., одна в 5, одна в 3 и одна в 1 рубль. Сидору верховой дал 20 руб.: две десятирублевки; Карпу — 15 руб.: десятирублевку и пятирублевку; Пахому — 12 руб.: десятирублевку и две рублевки (одну — найденную, другую — свою); Фоке — последнюю десятирублевку, а трехрублевку взял себе.
6. Мудрец пустился на уловку. Он прибавил к стаду на время своего верблюда, тогда их стало 18. Разделив это число, как сказано в завещании (старший брат получил 18 • 1/2 = 9 верблюдов, средний 18 • 1/3 = 6 верблюдов, младший 18 • 1/9 = 2 верблюда), мудрец взял своего верблюда обратно (9 + 6 + 2 + 1 = 18). Секрет, как и в предыдущей задаче, заключается в том, что части, на которые по завещанию должны были делить стадо сыновья, в сумме не составляют 1. Действительно, 1/2 + 1/3 + 1/9 = 17/18.
7. Если вода в бочке налита ровно до половины, то, наклонив бочку так, чтобы уровень воды пришелся как раз у края бочки, мы увидим, что высшая точка дна находится также на уровне воды (рис. а).

Это случится потому, что плоскость, проведенная через диаметрально противоположные точки верхней и нижней окружности бочки, делит ее на две равные части. Если вода налита менее чем до половины, то при таком же наклонении бочки из воды должна выступить часть дна (рис. б). Наконец, если воды в бочке более половины, то при наклонении дно окажется под водой (рис. в).
Рассудив именно так, работник справился с заданием.
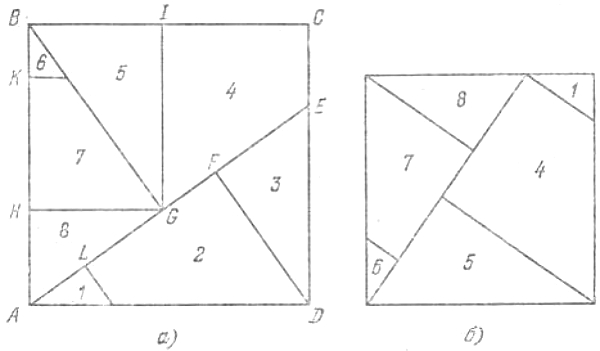
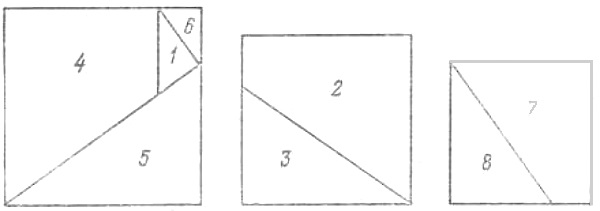
8. Решения приведены на рис. а и рис. б.
 |
 |
|
| а | б |
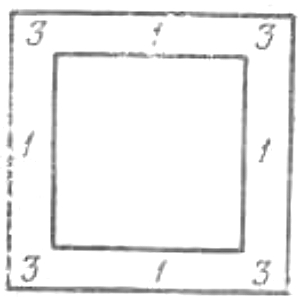
9. Слуга брал себе по бутылке из каждого среднего отделения и из тех же отделений, чтобы обмануть хозяина, после каждого воровства прибавлял по бутылке в угловые отделения. Так он воровал 4 раза по 4 бутылки, а всего, значит, унес 16 бутылок. Все это видно из рисунка.
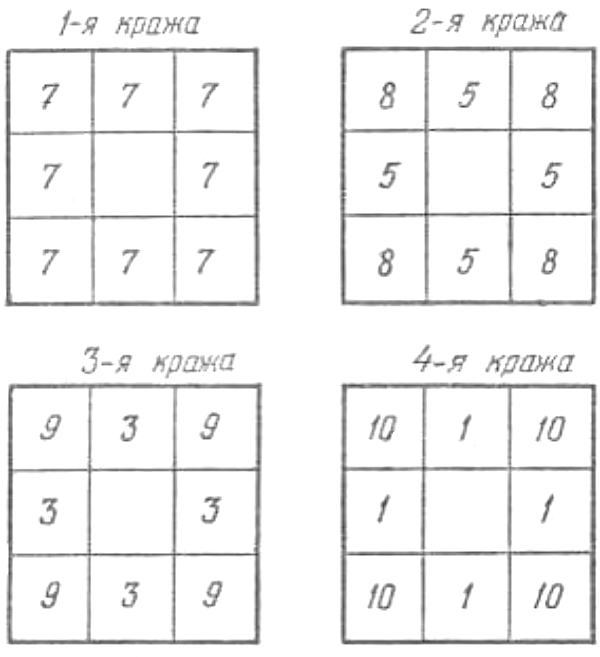
Слуга мог расставлять бутылки и другими способами. Но всегда в первом и третьем столбцах квадрата он должен был бы оставлять по 21 бутылке и потому не мог бы унести более 60 - 2 • 21 = 18 бутылок, т. е. совершить более четырех краж.
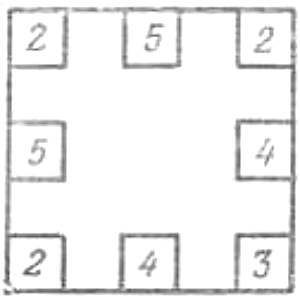
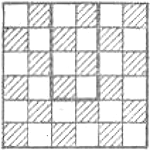
10. В первом случае в пещере остался 21 человек. Рассадить их с соблюдением условия, чтобы вдоль каждой стены находилось 9 человек, можно многими способами. Один из них показан на рисунке а.
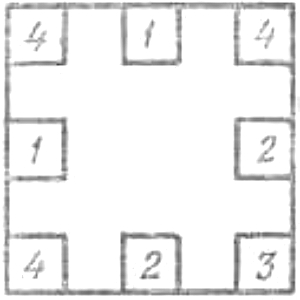 |
 |
|
| а | б |
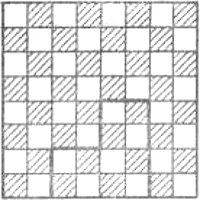
Во втором случае требуется рассадить 27 человек. Одно из возможных решений представлено на рис. б.
11. Нетрудно видеть, что третьему внуку дед дал грибов меньше всего, потому что третий внук должен был набрать еще столько же грибов, чтобы сравняться с братьями. Для простоты скажем, что третьему внуку дед дал грибов одну горсть.
Сколько же он дал таких же горстей четвертому?
Третий внук принес домой 2 горсти, потому что сам еще нашел столько же грибов, сколько дал ему дед. Четвертый внук принес домой ровно столько же грибов, сколько и третий, т. е. тоже 2 горсти; но он половину своих грибов растерял по дороге, значит, дед дал ему 4 горсти.
Первый внук принес домой 2 горсти, но из них 2 гриба он сам нашел, значит, ему дед дал 2 горсти без двух грибов. Второй внук принес домой 2 горсти, да по дороге он потерял 2 гриба; значит, дед ему дал 2 горсти да еще два гриба.
Итак, дед роздал внукам 1 горсть, да 4 горсти, да 2 горсти без двух грибов, да 2 горсти с двумя грибами, итого 9 полных горстей (в двух горстях не хватало по два гриба, зато в двух других горстях было по два лишних гриба). В 9 равных горстях было 45 грибов; значит, в каждой горсти 45 : 9 = 5 грибов.
Третьему внуку дед дал 1 горсть, т. е. 5 грибов; четвертому — 4 горсти, т. е. 5 х 4 = 20 грибов; первому — 2 горсти без двух грибов, т. е. (5 х 2) — 2 = 8 грибов; второму — 2 горсти с двумя грибами, т. е. (5 х 2) + 2 = 12 грибов.
12. Задача, очевидно, сводится к нахождению такого числа, которое делится нацело (т. е. без остатка) на 7, а при делении на 2, 3, 4, 5 и 6 дает в остатке 1.
Наименьшее число, которое делится без остатка на число 2, 3, 4, 5 и 6 (наименьшее кратное этих чисел), есть 60. Нужно, значит, найти такое число, которое делилось бы на 7 нацело и было бы вместе с тем на одну единицу больше числа, 1 делящегося на 60. Такое число можно найти путем последовательных попыток: 60, деленное на 7, дает в остатке 4, следовательно, 2 х 60 дает в остатке единицу
(2 х 4 = 8; 8 - 7 = 1).
Значит,
2 х 60 = числу, кратному 7 + 1,
откуда следует, что
(7 х 60 - 2 х 60) + 1 = числу, кратному 7,
т. е.
5 х 60 + 1 = числу, кратному 7,
5 х 60 + 1 = 301 .
Итак, наименьшее число, решающее задачу, есть 301. То есть наименьшее число яиц, которое могло быть в корзине у женщины, есть 301.
13. Вопрос, очевидно, сводится к тому, чтобы знать точное время при возвращении домой. Петр рассуждал так. Я завожу свои часы и перед уходом замечаю их показание, которое, положим, равно а. Приходя к знакомому, немедленно справляюсь у него о времени, и пусть его часы показывают b. Перед уходом от знакомого опять замечаю время по его часам, которые на этот раз показывают с. Придя домой, я немедленно замечаю, что мои часы показывают d. По этим данным легко определить искомое показание часов. Разность d - а покажет время моего отсутствия дома. Разность с - b — время, проведенное мною у знакомого. Разность (d - а) - (с - d), полученная от вычитания второго времени из первого, даст время, проведенное мною в дороге. Половина этого времени
| b + d - a - c |
| 2 |
употреблена мною на обратную дорогу. Прибавим эту половину к с, получим
| b + c + d - a |
| 2 |
это и будет точное показание часов при моем возвращении домой.
14. По условию вся вырученная сумма, очевидно, не превышает
9997 руб. 28 коп.
Значит, число проданных кусков не более
999728 : 4936,
т. е. не более 202 кусков.
Последняя цифра неизвестного числа кусков должна быть такова, чтобы она, будучи умножена на 6, давала произведение, оканчивающееся на 8; такая цифра может быть 3 или 8.
Положим, что последняя цифра неизвестного числа кусков равна 3. Стоимость трех кусков равна 14808 коп. Вычитая это число из вырученной суммы, мы должны получить число, оканчивающееся на 920.
Если предположить, что последняя цифра равна 3, то вторая от конца цифра может быть или 2, или 7, так как только эти цифры, будучи умножены на 6, дают произведения, оканчивающиеся на 2.
Положим, что неизвестное число оканчивается на 23. Вычитая стоимость 23 кусков из всей вырученной суммы, получим число, оканчивающееся на 200. Третья цифра может быть или 2, или 7; но так как неизвестное число не превосходит 202, то наше предположение неверно.
Если бы мы предположили, что неизвестное число оканчивается на 73, то третья цифра была бы равна 4 или 9; такое предположение тоже неверно.
Итак, последняя цифра не может быть 3; остается предположить, что она равна 8. Рассуждения, подобные предыдущим, покажут нам, что вторая цифра может быть или 4, или 9; из этих двух предположений верным может быть только второе.
Задача имеет одно решение: число проданных кусков равно 98, вся вырученная сумма равна 4837 руб. 28 коп.
15. Надо начинать счет с 6-го солдата, сидящего по левую руку от хозяина. Во втором же случае — с 5-го из солдат направо от хозяина.
16. В пылу спора кучер не смог представить, сколь велико количество запряжек, которые он должен сделать. Подсчитаем же мы это количество.
Обозначив лошадей цифрами 1, 2, 3, 4, 5, мы должны выяснить, сколькими способами можно переставить эти пять цифр.
Две цифры можно переставить двумя способами: (1, 2) и (2, 1). Перестановок из трех 1, 2, 3, начинающихся с цифры 1, будет также две. Но это число не зависит от того, какая фиксированная цифра из трех стоит на первом месте. Значит, всего перестановок из трех цифр будет 3 х 2 = 6:123 132 213 231 312 321
Продолжая далее, мы находим, что перестановок из четырех цифр с фиксированной первой цифрой будет 6 и множество всех перестановок из 4 цифр распадается на 4 группы по 6 перестановок, начинающихся с одной и той же цифры — 1, 2, 3 или 4. Так что всех перестановок будет 4 х 6 = 4 х 3 х 2 х 1 = 24. Аналогично, множество всех перестановок из 5 цифр состоит из 5 групп по 24 перестановки, начинающихся с одной цифры — 1, 2, 3, 4 или 5. Всего их будет 5 х 24 = 5 х 4 х 3 х 2 х 1 = 120.
Можно доказать, что множество перестановок из n цифр {1, 2, 3, ..., n} равняется произведению 1 х 2 х 3 ... n.
Это число обозначается n!
Вернемся к нашей задаче. Итак, кучеру предстояло сделать 120 перепряжек. Если он на каждую затратит только минуту времени, то на все ему понадобится 2 часа. Кучер проспорил.
17. Если один из мужчин купил, скажем, х предметов, то по условию он заплатил за них х2 копеек. Если его жена купила у предметов, то она заплатила за них у2 копеек. Значит, имеем х2 - у2 = 48, или (х - у) • (х + у) = 48.
Числа х, у по условию целые и положительные. Это возможно только в том случае, когда х - у и х + у четны и х + у > х - у . Разлагая 48 на сомножители, видим, что имеется только три удовлетворяющие этому условию возможности: 48 = 2 х 24 = 4 х 12 = 6 х 8, или
| { | х1 - у1 = 2, | { | х2 - у2 = 4, | { | х3 - у3 = 6, | ||
| х1 + у1 = 24, | х2 + у2 = 12, | х3 + у3 = 8. |
Решая эти системы уравнений, находим х1 = 13, у1 = 11, х2 = 8, у2 = 4, х3 = 7, у3 = 1.
Отыскивая те значения х и у, разность которых равна 9, находим, что Иван купил 13 предметов, Екатерина — 4 предмета. Точно так же Петр купил 8 предметов, Мария — 1 предмет. Таким образом, имеем следующие пары:
| { | Иван 13, | { | Пётр 8, | { | Алексей 7, | ||
| Анна 11; | Екатерина 4; | Мария 1. |
1. Положите кусок бумаги неправильной формы на стол и сделайте сгиб близ края. Пусть полученный при этом сгиб будет XX' (рисунок). Это прямая линия. Проведите ножом по сгибу и отделите меньшую часть куска. Таким образом вы получите прямолинейный край. Подобно предыдущему, согните бумагу по линии DY так, чтобы прямолинейный край XX' накладывался аккуратно сам по себе. Развернув затем бумагу, вы убедитесь, что сгиб DY идет под прямым углом к краю XX' так как наложение показывает, что угол YDX' равен углу YDX. Как раньше, проведите ножом по второй складке и удалите ненужную часть.

Повторяя указанный прием, вы получите края СВ и ВА. Наложение докажет, что углы А, В, С и D равны друг другу и прямые и что стороны ВС и CD соответственно равны DA и АВ. Итак, полученный кусок бумаги ABCD имеет форму прямоугольника. Наложение доказывает следующие его свойства:
1) четыре его угла все прямые;
2) четыре же стороны не все равны;
3) но две более длинные стороны равны между собой, а две более короткие — между собой.
2. Взяв прямоугольный кусок бумаги A'D'CB, складываем его наискось так, чтобы одна из коротких сторон, например СВ, легла на длинную ВА', как это показано на рисунке.

Угол В поместится на краю ВА' в точке А, конец перегиба по краю CD' получится в точке D. Сделаем затем перегиб через точки А и D), отогнув по прямой AD часть A'D'DA, которая выдается. Развернув после этого лист, найдем фигуру ABCD, которая и есть квадрат. В нем все углы прямые и все стороны равны.
3. Возьмем квадратный кусок бумаги и сложим его вдвое так, чтобы противоположные края его совпадали (рисунок). Получается сгиб, проходящий через середины двух других сторон и перпендикулярный к ним. На этой средней линии квадрата берем какую-нибудь точку и делаем такие сгибы, которые проходят через эту точку и через углы квадрата, лежащие по обе стороны средней линии. Таким образом получаем равнобедренный треугольник, в основании которого лежит сторона квадрата. Средняя линия делит, очевидно, равнобедренный треугольник на два совпадающих при наложении и прямоугольных треугольника. Она же делит угол при вершине равнобедренного треугольника пополам.

4. Возьмем на средней линии квадрата такую точку, чтобы расстояния ее от двух вершин квадрата были равны его стороне, и сделаем сгибы, как выше. В таком случае получим равносторонний треугольник (рисунок).

Требуемую точку на средней линии квадрата найти легко. Для этого надо над АА' поворачивать основание АС около одного из его концов А, пока другой его конец, С не упадет на среднюю линию в В.
5. Перегибаем квадрат через середины противоположных сторон (рисунок). Получаем линии АОВ и COD. На сгибах АО и ОВ строим известным нам уже способом равносторонние треугольники АОЕ, AON, BOF, BOG.

Делаем сгибы ЕF и NG.
Многоугольник AECFBGDN и будет правильным шестиугольником, в чем каждый без труда убедится сам. Наибольшее расстояние между точками многоугольника есть, очевидно, АВ.
6. Возьмем квадрат и известным уже нам способом посредством сгибов впишем в него другой квадрат (рисунок). Разделим пополам углы между сторонами данного и вписанного квадратов. Пусть сгибы, делящие эти углы пополам, пересекаются в точках E, F, G и H.

Полученный многоугольник AEBFCGDH и есть искомый правильный восьмиугольник. Действительно, треугольники ABE, BFC, CGD и DHA в нем равнобедренные и при наложении совпадают. Значит, стороны полученного восьмиугольника равны.
Углы многоугольника AEBFCGDH тоже равны. В самом деле, каждый из углов при вершинах Е, F, G, Н тех же треугольников равен полтора раза взятому прямому углу, так как углы при основании этих треугольников равны четверти прямого угла. Отсюда ясно, что и углы восьмиугольника при точках А, В, С и D также равны полтора раза взятому прямому углу каждый, т. е. все углы восьмиугольника равны между собой.
Сторона взятого квадрата а представляет наибольшее расстояние между точками восьмиугольника.
9. При решении этой задачи можно пользоваться листом картона или бумаги (лучше всего разлинованной на квадратные клетки). Как сделать требуемую вырезку, видно из рисунков a и b. Нетрудно видеть, что все четыре полученные из трех квадратов фигуры при наложении одной на другую совпадают.
|
|
|
|
|
a |
|
b |
10. Решение задачи видно из рисунке а, b.
|
|
|
|
|
a |
|
b |
Как ни проста и ни легка эта задача, но она представляет геометрическое толкование того, что 4 х 9 = 6 х 6. Кроме того, подобного рода задачи, прекрасно подготовляют к более сложным задачам о превращении одних фигур в другие посредством разрезания их на части и перекладывания этих частей. Желающий может сам придумать еще много подобных задач.
11. Решение задачи видно из прилагаемого чертежа (рисунок). Если зубчатую часть А вынуть из части В и затем снова вдвинуть ее между зубьев части В, передвинув на один зуб вправо, то получится безукоризненный прямоугольник и даже квадрат.
12. Решение задачи приведено на рисунке.

13. Решение задачи приведено на рисунке.
14. 1) Середины сторон квадрата соединим прямыми с противоположными вершинами квадрата;
2) из середин сторон квадрата проведем линии, параллельные проведенным линиям соединения, до встреч с другими линиями соединения;
3) в полученных прямоугольниках проведем диагонали, и тогда данный квадрат будет разбит на 20 прямоугольных треугольников, как можно видеть из рисунке.
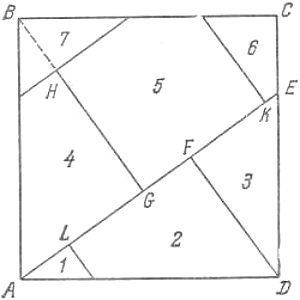
Нетрудно показать также, что в полученных прямоугольных треугольниках катеты таковы, что один вдвое больше другого. Из полученных 20 треугольников можно сложить 5 равных квадратов (рисунок).

15. На рисунках читатель найдет два решения этой задачи. Второе решение столь же просто, сколь и остроумно: задача решается проведением всего двух прямых линий.
16. Пусть ABCD (рисунок) — данный квадрат. Отложим на его стороне отрезок DE, равный половине диагонали этого квадрата. Соединим А с Е и на полученную прямую АЕ опустим перпендикуляры DF и BG. Затем откладываем отрезки GH, GK, FL, все равные DF; заканчиваем построение прямыми, параллельными или перпендикулярными DF, как показано на рисунке.
Если разрезать теперь квадрат по проведенным линиям и сложить затем все полученные части так, как указано на рисунке, то получим три искомых квадрата.

Математическое доказательство этого факта предоставляем читателю, заметив только, что, пользуясь подобием треугольников и теоремой Пифагора, доказанной в одной из предыдущих задач, нетрудно вывести, что 3 | DF |2 = | АВ |2.
17. Из прилагаемого чертежа (рисунок) видно, как нужно разрезать квадрат. Прямые DF и GB и точка L определяются так же, как и в предыдущей задаче.
Затем параллельно сторонам квадрата проводятся GH и GI (рис. а) и берется HK = GH. Таким образом получается 8 частей, из которых и составляются требуемые квадраты. Один из них представлен на рис. б, а другой есть средний на рисунке.
18. Квадрат разрезается точно так же, как в предыдущей задаче № 15. Из полученных 8 частей составляются 3 требуемых квадрата так, как на рисунке.

По данным решениям-рисункам нетрудно доказать математически правильность этих построений, что желающий вникнуть в сущность данной задачи пусть и сделает.
19. Разрезаем шестиугольник сначала по диагонали и складываем полученные 2 половины так, чтобы они образовали параллелограмм ABFE (рисунок). Из точки А, как из центра, радиусом, равным средней пропорциональной между длиной АЕ и высотой параллелограмма, проводим окружность, которая пересечет BF в точке G. Затем из точки Е опускаем перпендикуляр ЕН на продолжение AG и проводим прямую IК параллельно ЕН и на расстояния от нее, равном AG. Таким способом шестиугольник оказывается разрезанным на 5 таких частей, из которых можно образовать квадрат. Не разъясняем более этой задачи, так как предназначаем ее для знающих курс элементарной геометрии на плоскости.
1. Легко видеть, что получившиеся при разрезании квадрата треугольники А и В равны между собой. Также равны и трапеции С, D. Меньшее основание трапеций и меньший катет треугольников равны 3 см и поэтому должны совпасть при совмещении треугольника А с трапецией С и треугольника В с трапецией D. В чем же секрет? Его легко обнаружить, если посмотреть на рисунок.
Дело в том, что точки G, Н, Е не лежат на одной прямой,
tg ∠EHK = 8/3, а tg ∠ HGJ = 5/2.
Так как 8/3 - 5/2 = 1/6 > 0, то ∠EHK > ∠HGJ. Линия GHE является не прямой, а ломаной линией. Точно так же линия EFG — ломаная. Площадь полученного прямоугольника действительно равна 65 см2, но в нем имеется щель в виде параллелограмма, площадь которого в точности равна 1 см2. Наибольшая ширина щели равна, как легко видеть, 5 - 3 - (5 х 3)/8 = 1/8 сантиметра. Таким образом, хитрому плотнику все равно пришлось при починке замазывать небольшую щель.
Из тех же частей А, В, С, D можно сложить еще одну фигуру (рисунок).

Многоугольник KLGMNOFP может быть разложен на два прямоугольника размером 5х6 см2 и маленький прямоугольник размером 3х1 см2. Следовательно, его площадь равна 2 х 30 см2 + 3 см2 = 63 см2. Но, с другой стороны, он состоит из частей А, В, С, D, суммарная площадь которых, как мы знаем, равна 64 см2. Разгадка этого софизма опять заключена в том, что точки Е, F, G, Н не лежат на прямой линии. Подробное рассмотрение этого случая мы оставляем читателю.
2. Дело в том, что маленький прямоугольный треугольник не будет равнобедренным. Один из его катетов равен 1 см, а другой, как легко сосчитать, равен 8/7 см. Длина основания прямоугольника равняется не 9, а
8 см + 8/7 см = 91/7 см,
а его площадь
7 см х 91/7 см = 64 см2.
Противоречия не получается.
3. Более подробное рассмотрение того, как диагональ пересекает клетки прямоугольника (рисунок), показывает, что VRXS не есть квадрат.
Это можно подтвердить и с помощью вычислений.
Из подобных треугольников PQR и TQX получаем
PR : QR = ТХ : QX и
PR = (TX x QR) : QX = 11 x 1 : 13 = 11/13.
Значит, стороны прямоугольника VRXS равны 12 см и 1111/13 см, а площадь равна 12 см x 1111/13 = 1422/13 см2. Площадь треугольника STU равна площади треугольника PQR и равна 1/2 x 1 см x 11/13 см = см2. Таким образом, площадь фигуры равняется
1422/13 см2 + 211/26 см2 = 143 см2.
4. «Здравый смысл» подсказывает такой ответ: «Конечно, у апельсина образуется больший зазор, чем у Земли! Ведь в сравнении с окружностью земного шара — 40 000 км — какой-нибудь один метр есть столь ничтожная величина, что прибавка ее останется совершенно незаметной. Другое дело апельсин: по сравнению с его окружностью один метр — огромная величина, и прибавка ее к длине окружности должна быть весьма ощутима».
Однако давайте проверим наше заключение с помощью вычислений. Пусть длина окружности земного шара равна С, а апельсина с метрам. Тогда радиус Земли R = C/2π и радиус апельсина r = c/2π. После прибавки к обручам одного метра окружность обруча у Земли будет С + 1, а у апельсина с + 1, радиусы их соответственно будут (C + 1) : 2π и (c + 1) : 2π. Если из новых радиусов вычтем прежние, то получим в обоих случаях одно и то же приращение:
(C + 1) : 2π - C : 2π = 1 : 2π для Земли,
(с + 1) : π - с : 2π = 1 : 2π для апельсина.
Итак, у Земли и у апельсина получится один и тот же зазор в 1/2π метра, т. е. примерно 16 см. Столь «поразительный» результат есть следствие постоянства отношения длины любой окружности к ее радиусу.
1. «Фокуса» здесь, конечно, нет, а есть только правильный математический расчет.
Чтобы от 5 прийти к 9, нужно считать так: 5, 6, 7, 8, 9. Значит, от 9 до 5 нужно пройти через те же числа 9, 8, 7, 6, 5, только считая их в обратном порядке. Если, указав на 9, мы скажем «пять», затем, указывая на 8, скажем «шесть» и т. д., то, придя к задуманному числу 5, скажем «девять». Если затем идти по кругу в том же направлении и присчитать к «девяти» еще 12 последовательных чисел круга, то опять приходим к тому же числу 5.
Дело сводится, следовательно, к счету по кругу в обратном направлении от указанного числа 9 до 9 + 12, т. е. до 21.
Если, наоборот, задумано 9, а указано 5, то от 9 до 5, считая в прямом направлении по кругу (по порядку возрастания чисел), получаем: 9, 10, 11, 12, 12 + 1, 12 + 2, 12 + 3, 12 + 4, 12 + 5, т. е. 17. Следовательно, начиная с 5, можно прийти к задуманному числу 9, идя в обратном направлении и отсчитывая те же 5 + 12 = 17 чисел.
2. Пусть у партнера в руках по n спичек (причем n ≥ Ь) и вы предлагаете ему переложить из правой руки в левую а спичек (причем а < 6). Тогда до перекладывания в обеих руках у него по n предметов (причем n > а), после первого перекладывания — в левой n + а, в правой n - а предметов, после второго перекладывания — в левой (n + а) - (n - а) = 2а, в правой n - а предметов и, наконец, в левой 2а предметов, а правая рука пуста.
3. Двузначное число представимо в виде 10а + b, где 0 < а ≤ 9 — число десятков, 0 ≤ b ≤ 9 — число единиц. Разность имеет вид
10а + b - (10b + а) = 9 (а — b),
т. е. делится на 9. Если эта разность равна 10k + l (k ≤ 9, l ≤ 9), то 10k + l = 9k + (k + l) и, значит, k + l = 9. Итак, первую цифру разности можно найти, вычитая из 9 цифру, названную вам.
Например, если задумано число 37, то имеем: 73 - 37 = 36. Вам сообщают цифру 6, и вы находите первую цифру: 9 - 6 = 3. Еще один пример: 54 - 45 = 9. Последняя цифра 9, значит, первая равна 9 - 9 = 0, т. е. разность равна 9.
4. Частное равняется указанной вами разности между крайними цифрами числа, умноженной на 11. Например, если взять сначала число 845, то 845 - 548 = 279, 279 : 9 = 33 = (8 — 5) • 11.
Чтобы доказать это правило, заметим, что каждое трехзначное число можно представить в виде 100а + 10b + с, где 0 < а ≤ 9 — число сотен, b ≤ 9 — число десятков и с ≤ 9 - число единиц во взятом числе. Тогда число с переставленными цифрами будет равно
100c + 10b + а.
Вычитая второе из первого и деля на 9, имеем
|
100a + 10b + c - (100c + 10b + a) |
= | 99(a - c) | = 11 • (a - c). |
| 9 | 9 |
5. Из решения предыдущей задачи мы знаем, что разность между любым трехзначным числом и числом, полученным из него перестановкой крайних цифр, всегда делится на 99. Так как крайние цифры отличаются более чем на единицу, то эта разность обязательно будет трехзначным числом, обозначим ее
100k+ 10l+ m(0 < k ≤ 9, l ≤ 9, m ≤ 9). Имеем
100k + 10l + m = 99k + (10l + m + k).
Так как разность делится на 99, то это равенство показывает, что обязательно 10l + m + k = 99, откуда вытекает, что l = 9, m + k = 9. Число с переставленными крайними цифрами имеет вид 100m + 10l+ k, и сумма равняется
100k + 10l + m + 100m + 10l + k = 100(k + m) + 20 • l + (m + k) = 100 • 9 + 20 • 9 + 9 = 1089.
6. Над задуманным числом n совершаются следующие действия:
n • 2 + 5 = 2n + 5, (2n + 5) • 5 = 10n + 25,
10n + 25 + 10 = 10n + 35, (10n + 35) • 10 = 100n + 350,
100n + 350 - 350 = 100n, 100n : 100 = n.
То есть всегда получится задуманное число.
Рассматривая решение этой задачи, нетрудно понять, что ей можно придать любое число различных видоизменений. Так, например, если пожелать, чтобы всегда в результате число сотен выражало задуманное число и чтобы приходилось умножать всегда на 2, 6 и 10, но вычитать приходилось бы не 350, как в приведенной задаче, а другое число, то нужно принять во внимание, как получилось в вышеприведенной задаче 350. Это число произошло так: прибавлено 5, да умножено на 5, итого 25; к этому числу прибавлено 10, получилось 35; умножив же это число на 10, получаем 350. Следовательно, если захотеть вместо 350 вычитать из окончательного результата другое число, то и задавать нужно прибавлять не 5 и 10, а другие числа. Зададим, например, вместо 5 прибавить 4, а вместо 10 прибавить 12. Ясно, что из последнего полученного числа придется вычесть 320(4 • 5 = 20; 20 + 12 = 32; 32 • 10 = 320), и тогда получим остаток, число сотен которого и даст нам задуманное число.
Таким образом, задачу можно видоизменять до бесконечности.
Точно так же легко заметить, что, умножая задуманное число на 2, на 5 и на 10, мы умножаем его, в сущности, на 100 (2 • 5 • 10 = 100). Поэтому, если мы опять-таки хотим, чтобы число сотен окончательного результата показывало задуманное число, — все равно, какие множители выбрать, лишь бы умножение на них давало в окончательном результате умножение на 100. Отсюда следует, что оставляя те же множители 2, 5, 10, можно изменить их порядок, т. е. сначала умножить, например, на 5, потом на 10, а затем на 2 и т. д.
Точно так же вместо множителей 2, 5, 10 можно брать другие, дающие в произведении 100, например: 5, 4, 5 или 2, 2, 25 и т. д. Нужно помнить только при этом, конечно, что всем этим изменениям множителей и прибавляемых чисел соответствует изменение числа, которое в конце нужно вычесть. Так, например, будем умножать на 5, 4, 5, а прибавлять числа 6 и 9, и пусть задуманное число будет 8.
Умножив на 5, получим 40; прибавив 6, получим 40 + 6 = 46; умножив на 4, получим 160 + 24 = 184; прибавив 9, получим 160 + 33 = 193; умножив это число на 5, получим 800 + 165 = 965, т. е. для получения числа сотен, показывающего задуманное число, нужно отнять в данном случае 165 (6 • 4 = 24; 24 + 9 = 33; 33 • 5 = 165).
Можно также взять не 100, а любое иное число и сделать так, чтобы оно заключалось в остатке от последнего вычитания столько раз, сколько единиц заключается в задуманном числе. Так, например, возьмем число 24, которое можно представить состоящим из множителей 2, 3, 4 ( 2 • 3 • 4 = 24) а числа, которые будем прибавлять, пусть будут 7 и 8.
Пусть задуманное число есть 5. Удваивая его, находим 10, прибавляя 7, находим 10 + 7 = 17; утраивая, находим (10 + 7) • 3 = 30 + 21 = 51; прибавляя 8, находим 30 + 29 = 59; беря последнее число 4 раза, получим 120 + 116 = 236. Отнимаем отсюда 116, остается 120, в котором 24 содержится 5 раз, т. е. получается задуманное число 5.
Можно также вместо трех множителей брать только два, а вместо двух чисел прибавлять только одно, и тогда число десятков числа, полученного после вычисления, подобного предыдущему, покажет задуманное число.
Можно также брать четыре, пять, шесть и т. д. множителей, прибавлять соответствующее (три, четыре и т. д.) количество чисел, затем, поступая, как указано выше, угадывать задуманное кем-либо число.
Можно, наконец, вместо того, чтобы прибавлять числа, вычитать их, а в конце вместо вычитания прибавлять известное число. Так, например, воспользуемся числами первого примера настоящей задачи, и пусть задуманное число будет 12. Удвоив его, получим 24; вычитая отсюда 5, получим 24 — 5; умножая на 5, получим 120 — 25; вычитая 10, получим 120 — 35; умножая на 10, получим 1200 — 350. Здесь вместо того, чтобы вычесть, нужно прибавить 350: сумма получится 1200, и число сотен в ней (12) дает задуманное число.
Словом, читатель может видоизменять и разнообразить эту задачу как ему угодно.
7. Секрет разгадывания с виду прост: обратите внимание на цифры, написанные в самой нижней графе. Если вам скажут, например, что задуманное число находится во 2-м, 3-м и 5-м столбцах, считая справа (или на 2-й, 3-й, 5-й пластинках веера), то 168 сложите числа, стоящие в этих столбцах внизу, получите 22 (2 + 4 + 16), и будьте уверены, что задумано именно это, а не иное какое-нибудь число).
Еще пример — число 18. Вы найдете его во 2-м и 5-м столбцах. Внизу этих столбцов стоят числа 2 и 16; сложенные вместе, они дают действительно 18.
Как же составляется подобная таблица?
Если написать ряд чисел, начиная с 1, таких, чтобы каждое было вдвое больше предыдущего, т. е. 1, 2, 4, 8, 16, 32, . . . , то ряд этот обладает тем замечательным свойством, что каждое целое положительное число может быть получено, и не более чем одним способом, как сумма некоторых членов ряда. Например, 27 = 16 + 8 + 2 + 1 . Для составления таблицы мы взяли только начальные члены ряда: 1, 2, 4, 8, 16 (20, 21, 22, 23, 24), сложением которых можно получить все числа от 1 до 31 (= 25 - 1). За каждым из них закреплен определенный столбец таблицы (см. нижнюю строку). Воспользовавшись указанным выше свойством ряда степеней двойки, мы помещаем каждое целое число в те столбцы, в основании которых стоят степени двойки, в сумме составляющие эго число. Так 27 попадает в столбцы с основаниями 1, 2, 8, 16. Теперь ясно, почему для угадывания достаточно сложить числа, стоящие внизу столбцов. Можно воспользоваться этим свойством степеней двойки для обозначения чисел. Напишем для каждого числа последовательность из 0 и 1 такую, что на первом месте справа стоит 1 или 0 в соответствии с тем, содержится наше число в первом столбце или нет, на втором 1 или 0 в зависимости от того, стоит ли число во втором столбце, и так далее. Например, число 27 обозначается этим способом так: 1 1 0 1 1, а число 12 — так: 0 1 1 0 0. Условимся не писать нули, стоящие слева, тогда для числа 12 получим представление 1100.
Такой способ записи называется двоичной системой изображения чисел.
Для того чтобы изобразить число с его помощью, совсем не обязательно иметь перед глазами таблицу. Достаточно представить целое число в виде суммы степеней двойки и на местах, номера которых (считая справа налево, начиная с 0) участвуют в этом представлении, поставить 1, а на остальных местах 0:
|
Число |
|
Двоичное изображение |
|
2 = 21 |
|
10 |
|
3 = 21 + 20 |
|
11 |
|
5 = 22 + 20 |
|
101 |
|
19 = 24 = 21 + 20 |
|
10 010 |
|
134 = 27 + 22 + 21 и т. д. |
|
10 000 110 и т. д. |
Двоичная система очень удобна для представления чисел в вычислительных машинах, так как для записи любого числа достаточно только двух знаков — 0 и 1. В общеупотребительной же десятичной системе для этого требуется 10 знаков — 0, 1, 2, . . ., 8, 9.
8. Если задумано четное число 2n, то, проделав с ним указанную последовательность действий, получим
2n • 3 = 6n, бn : 2 = 3n, 3n • 3 = 9n, 9n : 9 = n.
Удваивая частное n, получаем задуманное число 2n.
Проверим правило для нахождения задуманного числа в общем случае. Если задумано число четное, проверка уже сделана. Пусть теперь задумано нечетное число 2n + 1. Наши действия принимают вид
(2n + 1) • 3 = 6n + 3.
Поскольку это число на 2 не делится, то, прибавляя 1, находим 6n + 3 + 1 = 6n + 4. Разделив это число на 2, получим 3n + 2. Далее, (Зn + 2) • 3 = 9n + 6.
Частное от деления 9n + 6 на 9 равно n (а остаток равен 6). Удваивая это частное и прибавляя 1, находим задуманное число 2n + 1.
9. Всякое число может быть представлено в одной из следующих форм: 4n, 4n + 1 , 4n + 2, 4n + 3, где букве n нужно придавать значения 0, 1, 2, 3, 4 и т. д.
1) Возьмем сначала число вида 4n и произведем над ним указанные выше действия. Получается
| 4n • 3 = 12n, | 12n : 2 = 6n, | 6n • 3 = 18n, | ||
| 18n : 2 = 9n, | 9n : 9 = n, | 4 • n = 4n. |
2) Для числа вида 4n + 1 получим
| (4n + 1) • 3 = 12n + 3 | (12n + 3 + 1) : 2 = 6n + 2, | |
| (6n + 2) • 3 = 18n + 6, | (18n + 6) : 2 = 9n + 3. |
Частное от деления 9n + 3 на 9 равно n, и, пользуясь правилом, мы угадываем число 4n + 1.
3) Для числа вида 4n + 2 имеем
(4n + 2) • 3 = 12n + 6, (12n + 6) : 2 = 6n + 3,
(6n + 3) • 3 = 18n + 9, (18n + 9 + 1) : 2 = 9n + 5.
Частное от деления 9n + 5 на 9 равно n и, прибавляя к 4n число 2 (деление нацело не выполнялось только во второй раз), получаем задуманное число.
4) Для числа вида 4n + 3 имеем
(4n + 3) • 3 = 12n + 9, (12n + 9 + 1) : 2 = 6n + 5,
(6n + 5) • 3 = 18n + 15, (18n + 15 + 1) : 2 = 9n + 8.
Частное от деления 9n + 8 на 9 равно n и, поступая с ним, как указано в условии, находим задуманное число 4n + 3.
Таким образом, всегда получается задуманное число.
11. Обращаясь к решению задачи 9, находим, что для числа вида 4n окончательный результат вычисления дает 9n, т. е. число, кратное 9. Следовательно, сумма цифр этого числа должна делиться на 9, а отсюда заключаем, что неизвестная нам цифра такова, что, сложив ее с остальными известными цифрами, мы должны получить число, делящееся на 9 (т. е. кратное 9). Если же сумма известных цифр кратна 9, то значит, неизвестная цифра сама есть 9, ибо нам дано, что она не нуль.
Для числа вида 4n + 1 результат вычислений есть 9n + 3; прибавляя сюда 6, получаем число, кратное 9, т, е. кратна 9 и сумма его цифр.
Для числа вида 4n + 2 результат вычислений дает 9n + 5; прибавляя 4, получаем число, кратное 9, следовательно, и сумма его цифр должна быть кратной 9.
Наконец, для числа вида 4n + 3 окончательный результат вычислений дает 9n + 8. Прибавляя 1, находим число, кратное 9. Сумма его цифр также должна быть кратна 9.
Итак, указанные нами выше правила верны.
12. Если над каким-либо числом n производится ряд умножений и делений, то получается результат вида
| n | abc ... |
.
|
| ghk ... |
Если произвести тe же действия над числом р, то получится результат вида
| p | abc ... |
.
|
| ghk ... |
Оба эти результата, разделенные первый на n, а второй на p, дадут, очевидно, одно и то же число
| abc ... |
.
|
| ghk ... |
Итак, зная число
| abc ... |
.
|
| ghk ... |
и сумму
| abc ... |
+n.
|
| ghk ... |
достаточно из последней вычесть первое, чтобы получить число n.
Можно, очевидно, всячески видоизменять настоящую задачу, так как, во-первых, можно делить и умножать на какие угодно числа, а во-вторых, вместо того, чтобы умножать и делить поочередно, можно сначала умножать два, три и т. д. раза подряд, затем столько же раз делить или наоборот. Можно также, зная последнее частное, заменять сложение вычитанием, если задуманное число окажется меньше полученного последнего частного, и т. д.
13. I. Пусть задуманные числа a, b, с, d, е. Даны суммы а + b, b + с, c + d, d + e, е + а . Складывая суммы, стоящие на нечетных местах, получим а + Ь + с + d + е + а и, складывая суммы, стоящие на четных местах, получим b + с + d + е.
Вычитая из первой суммы вторую, получаем 2а, Половина этого числа есть первое из задуманных чисел а. Вычитая а из а + b, получим b и т. д.
II. Пусть задуманы числа а, Ь, с, d, е, f. Даны суммы a + b, b + с, с + d, d + e, e + f, f + b. Суммы, стоящие на нечетных местах, за исключением первой, дают c + d + e + f. Суммы, стоящие на четных, местах, дают b + c + d + e + f + b. Разность между этой суммой и предыдущей есть 2b; половина этого числа и есть задуманное второе число b, Остальные числа найти уже легко.
Можно эти задачи решать иными способами, из которых укажем на следующие.
Пусть число задуманных чисел будет нечетное.
Сложив все данные суммы и разделив полученное число пополам, найдем сумму всех задуманных чисел. Если же задумано четное число чисел, то сложим все данные суммы, кроме первой, результат поделим пополам и получим сумму всех задуманных чисел, кроме первого. Но, зная сумму всех задуманных чисел, легко найти в данном случае каждое число в отдельности. Пусть, например, задуманы числа 2, 3, 4, 5, 6. Суммы, которые даются, будут: 5, 7, 9, 11, 8. Складывая эти числа, получим 40. Половина этого числа (20) и есть сумма всех задуманных чисел.
Зная теперь, что сумма 2-го и 3-го задуманных чисел есть 7, а сумма 4-го и 5-го чисел есть 11, вычитаем 7 + 11 = 18 из 20 и получаем первое задуманное число 2 и т. д.
Подобным же образом надо поступать и в том случае, когда задумано четное число чисел.
Можно узнавать числа и так. Если кто-либо задумает 3 числа, предложите ему сказать их суммы по два, как объяснено выше; если он задумал 4 числа, предложите ему сложить их по три и сказать вам суммы; если задумано 5 чисел, предложите сложить их по четыре и сказать вам суммы и т. д. Затем, чтобы отгадать задуманные числа, нужно руководствоваться следующим общим правилом.
Все известные суммы сложить и полученный результат разделить на число, единицей меньшее числа задуманных чисел. Полученное частное и есть сумма всех задуманных чисел. После этого уже нетрудно найти каждое число в отдельности. Пусть, например, задуманы 3, 5, 6, 8. Суммы по три будут 3 + 5 + 6 = 14, 5 + 6 + 8 = 19, 6 + 8 + 3 = 17, 8 + 3 + 5 = 16. Складывая эти суммы, получаем 66. Эту сумму надо разделить на 3 (т. е. на число, единицей меньшее числа задуманных чисел). Получается 22 — сумма всех задуманных чисел. Если теперь из 22 вычесть 14, получим последнее из задуманных чисел (8); вычитая 19, получаем первое (3) и т. д. Понять и доказать все это нетрудно.
Желающим предоставляем доказать, что в случае четного числа задуманных чисел нельзя брать попарно суммы так, чтобы последняя состояла из последнего задуманного чиcла плюс первое, а непременно надо так, чтобы складывать последнее и второе из задуманных чисел.
14. Действия, которые производятся в данном случае над задуманным числом n, можно выразить так: (na + b) : c, а это выражение можно представить na : c + b : c. Ясно, что, вычитая n • a : c, получим остаток b : с.
15. Число, которое умножается на 2, дает всегда четное произведение. Следовательно, сумма обоих произведений четна или нечетна, смотря по тому, будет ли четное или нечетное другое произведение. Но если число множится на нечетный множитель, то произведение будет четным, если множимое четно, и нечетным, если нечетно множимое. Итак, по сумме обоих произведений можно судить, четно или нечетно то число, которое множится на нечетный множитель.
16. Пусть А и В — взаимно простые числа и два других а и с — тоже взаимно простые числа, причем А кратно числу а. После соответствующих умножений может получиться сумма Ас + Ва или Аа + Вс. Ясно, что первая сумма делима на а, вторая же — нет. Следовательно, В умножится или не умножится на а, смотря по тому, делима или неделима на а сумма, полученная задумавшими после соответствующих умножений и сложения.
17. Пусть задуманные числа будут а, b, с, d, . . . Над ними производятся следующие действия:
для первых двух чисел:
(2а + 5) • 5 = 10а + 25, 10а + 25 + 10 = 10а + 35,
10а + 35 + b = 10а + b + 35;
для третьего числа:
(10а + b + 35) • 10 + с = 100а + 10b + с + 350;
для четвертого:
(100a + 10b + c + 350) • 10 + d = 1000a + 100b + 10c + d + 3500 и т. д.
Отсюда ясно, что, вычитая из результата 35, 350, 3500, смотря по количеству задуманных чисел, мы получим все задуманные числа в виде цифр остатка, считая слева направо.
1.
![]()
2.
| 2 = | 5 + 5 |
| 5 |
3.
| 4 = 5 - | 5 |
| 5 |
4.
| 5 = 5 + 5 - 5 = 5 • | 5 |
| 5 |
5.
![]()
6. Эта задача сложнее предыдущих, Вот некоторые из ее решений:
31 = 33 + 3 + 3/3, 31 = 33 - 3 + 3/3, 31 = 33 - (3 + 3) : 3.
7. 100 = 5 • (-2 + 4 ) • (1 + 2 + 7).
8. Чтобы быть победителем, старайтесь только, чтобы вам удалось назвать число 89. Ясно, что, если вы назовете это число, то какое бы число (десять или меньше) ни прибавил ваш противник, вы тотчас найдете соответственное число, добавив которое к полученному противником вы получаете сто и выигрываете.
Но, чтобы суметь наверняка сказать «89», а потом, значит, и «100», постарайтесь разобраться в следующих очень нетрудных рассуждениях. Начнем отнимать, сколько возможно, от ста по одиннадцати. Получим ряд таких чисел: 89, 78, 67, 56, 45, 34, 23, 12, 1. Или же, если напишем их в порядке возрастания, получим
1, 12, 23, 34, 45, 56, 67, 78, 89.
Запомнить эти числа очень легко: стоит только взять предельное число, т. е. 10, и прибавить к нему 1 — получится 11. Затем берем это число и все числа, составленные умножением 11 на 2, на 3, на 4, . . . , на 8, — получим 11, 22, 32, 44, 55, 66, 77, 88; увеличим каждое из этих чисел единицей и начнем единицей же ряд. Получим опять-таки предыдущий, уже написанный нами ряд чисел:
1, 12, 23, 34, 45, 56, 67, 78, 89.
Ясно теперь, если вы скажете «1», то какое бы число (по условию не больше 10) ни назвал другой играющий, он не помешает вам сказать «12»; точно так же вы всегда можете назвать 23, а затем 34, 45, 56, 67, 78 и 89.
Когда вы скажете «89», то, какое бы число (не большее 10) ни назвал ваш соперник, вы говорите «сто» и выигрываете.
Отсюда видно также, что если оба играющих знают, в чем дело, то выигрывает всегда тот, кто первый скажет «один», т. е. тот, кто начинает игру.
9. Если вы хорошо усвоили решение предыдущей задачи, то нетрудно видеть, как надо поступать в каждом отдельном случае. Пусть, например, назначенное число будет 120; предельное, как и выше, равно 10. Тогда, очевидно, нужно иметь в виду числа 109, 98, 87, 76, 65, 54, 43, 32, 21, 10, т. е. начиная с 10, все кратные 11, увеличенные на 10. Отсюда также видно, что знающий решение этой задачи выигрывает всегда, если он начинает. Пусть, например, заданное число будет 100, но предельное число есть не 10, а 8. В таком случае нужно иметь в виду числа 91, 82, 73, 64, 55, 46, 37, 28, 19, 10, 1, т. е. начиная от единицы, все числа, кратные 9 и увеличенные на единицу. И в данном случае знающий задачу всегда выигрывает, если он начинает.
Но если принять за предельное число, например, 9, то числа, которые нужно иметь в виду, будут 90, 80, 70, 60, 50, 40, 30, 20, 10. И ясно, что начинающий здесь может проиграть, если другому известен секрет, ибо, какое бы число начинающий ни сказал, он не может помешать другому назвать 10, 20 и т. д. — все числа до 100.
10. Можно перекладывать спички так: 4 к 1, 7 к 3, 5 к 9, 6 к 2, 8 к 10 — или иначе: 7 к 10, 4 к 8, 6 к 2, 1 к 3 и 5 к 9.
11. Обозначим положенные в ряд спички номерами 1, 2, 3, . . . 15. Тогда задача решается путем следующих 12 перекладываний: 2 к 6, 1 к 6, 8 к 12, 7 к 12, 9 к 5, 10 к 5, 4 между 5 и 6, 3 между 5 и 6, 11 между 5 и 6, 13 на место с номером 11, 14 на то же место, 15 на то же место.
12. Чтобы показать процесс правильного перенесения кружков, обозначим кружки цифрами 1, 2, 3, . . . , 7, 8, начиная с наименьшего, затем изобразим процесс перенесения таблицей:
| Палочка А | Вспомогательная палочка | Палочка В | |
|
До начала После 1-го перенесения » 2-го » » 3-го » » 4-го » » 5-го » » 6-го » » 7-го » » 8-го » » 9-го » » 10-го » » 11-го » » 12-го » » 13-го » » 14-го » » 15-го » |
1, 2, 3, 4, 5, 6, 7, 8 2, 3, 4, 5, 6, 7, 8 3, 4, 5, 6, 7, 8 3, 4, 5, 6, 7, 8 4, 5, 6, 7, 8 1, 4, 5, 6, 7, 8 1, 4, 5, 6, 7, 8 4, 5, 6, 7, 8 5, 6, 7, 8 2, 5, 6, 7, 8 1, 2, 5, 6, 7, 8 1, 2, 5, 6, 7, 8 2, 5, 6, 7, 8 5, 6, 7, 8 5, 6, 7, 8 |
- 1 1 - 3 3 2, 3 1, 2, 3 1, 2, 3 2, 3 3 3 - 1 - |
- - 2 1, 2 1, 2 2 - - 4 1, 4 1, 4 4 3, 4 3, 4 2, 3, 4 1, 2, 3, 4 |
Отсюда мы видим, что на палочку III, когда она свободна, надеваются только нечетные кружки (1-й, 3-й, 5-й и пр.), а на В — только четные. Так что, например, для перенесения четырех верхних кружков нужно было сначала перенести три верхних на вспомогательную палочку — что, как видно из таблицы, потребовало семи отдельных перекладываний, — затем мы перенесли 4-й кружок на третью палочку — еще одно перекладывание — и, наконец, три верхних кружка со второй палочки перенесли на ту же третью поверх 4-го кружка (причем 1-я палочка играла у нас роль вспомогательной), что опять потребовало семя отдельных перекладываний.
Итак, вообще, чтобы при таких условиях перенести колонну из n каких-нибудь кружков, расположенных вертикально в убывающем порядке, нужно сначала перенести колонну из (n - 1) верхних кружков на одно из свободных мест, потом основание, т. e. n-й кружок, на другое свободное место и, наконец, на то же место опять всю колонну из (n - 1) верхних кружков.
Обозначая число необходимых отдельных перенесений буквою Π со значком, соответствующим числу кружков, имеем, следовательно,
Πn = 2Пn -1 + 1.
Понижая значение n до единицы и делая подстановку, легко находим
Πn = 2n - 1 + 2n - 2 + . . . + 23 + 22 - 21 + 20.
Получаем, следовательно, сумму геометрической прогрессии, которая дает
Πn = 2n - 1 .
Таким образом, в случае детской пирамиды из 8 кружков нужно сделать 28 - 1, или 255, отдельных перекладываний кружков.
Допустим, что перенос одного кружка продолжается всего одну секунду, тогда на перемещение пирамиды из восьми кружков потребуется 4 минуты с лишком. Что же касается переноса башни из 64 кружков, то на это понадобится
18 446 744 073 709 551 615 сек.
А это значит, ни более и ни менее, как пять с лишним миллиардов веков.
13. Ответ на вопрос неожиданно оказывается связанным с двоичной системой изображения чисел (см. решение задачи в главе "Угадывание чисел" № 7). Представим каждое из чисел 12, 10, 7 в двоичной системе:
12 — 1100
10 — 1010
7 — 111
В каждом столбце получившейся таблицы, за исключением крайнего правого, стоит по две единицы. Первым ходом игрок А делает так, чтобы в каждом столбце стояло по две единицы или ни одной;
12 — 1100
10 — 1010
6 — 110
Своим ходом игрок Б нарушает это свойство, а игрок А его опять восстанавливает:
1 — 1
7 — 111
6 — 110
Если мы проследим за игрой далее, то увидим, что каждым ответным ходом игрок А восстанавливает нарушенное предыдущим ходом Б свойство таблицы содержать в каждом столбце четное количество единиц.
Назовем систему из трех целых неотрицательных чисел правильной, если после представления каждого числа в двоичной системе любой столбец содержит четное количество единиц, и неправильной в противном случае.
Легко видеть, что правильная система после любого хода становится неправильной, а из любой неправильной системы одним ходом всегда можно сделать правильную. Для этого давайте выберем самый левый столбец, где стоит нечетное число единиц, и то из чисел, которое в этом столбце имеет единицу, заменим на меньшее так, чтобы получилась правильная система. Это, очевидно, всегда можно сделать.
Если исходная система чисел неправильная (как в нашем примере), то начинающий игру всегда будет в выигрыше. Для этого он должен каждым своим ходом делать правильный набор чисел. Если же исходная система правильная (например, 12, 10, б или 13, 11, 6), то ваш противник, если он знает секрет игры, выиграет у вас, как бы вы ни играли. В этом случае делайте произвольные ходы в надежде, что противник ошибется и после его хода система чисел станет неправильной. Тогда перехватывайте инициативу и доводите игру до победного конца.
Можно раскладывать спички на 4, 5 и более кучек.
Вы выиграете, если будете играть так, чтобы после каждого вашего хода в любом столбце таблицы стояло четное число единиц.
1. Все дело в том, чтобы приготовляясь к «угадыванию» и переворачивая косточки домино «лицом» вниз, тринадцать из них расположить в таком последовательном порядке, как на рисунке.

Ряд этих косточек, как видим, представляет ряд первых двенадцати натуральных чисел да еще нуль:
12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0,
и числа эти идут в убывающем порядке. Справа за этим рядом вы помещаете (тоже «лицом» вниз) еще 12 косточек в каком угодно порядке. Если теперь вы уйдете в другую комнату, а кто-нибудь переместит справа налево несколько (менее 12) косточек и приставит их так, чтобы они шли за (6, 6) влево, то, возвратись, вы откроете среднюю (т. е. 13-ю по счету, считая слева) косточку в ряду, и на ней будет как раз столько очков, сколько было перемещено в ваше отсутствие косточек.
Почему так, нетрудно разобраться. Когда вы уходите в другую комнату, то вы знаете, что в середине ряда перевернутых «изнанкой» вверх косточек домино лежит пустая косточка, т. е. (0, 0). Представим теперь, что перемещена в ваше отсутствие с правого конца на левый одна косточка. Какая тогда косточка будет находиться в середине? Очевидно, (0, 1), т. е. единица. А если переместить две косточки, то в середине будет находиться косточка с двумя очками; если переместить три косточки, то в середине будет косточка с тремя очками и т. д. Словом, средняя косточка обязательно верно покажет вам число перемещенных справа на левый конец косточек домино. (Перемещаются, что надо всегда помнить, не более 12 косточек.)
Игру можно продолжать. Опять уйти в другую комнату и попросить кого-либо переместить с правого конца на левый еще несколько косточек. Возвратись в комнату, вы откроете косточку, указывающую число перемещенных косточек. Она будет теперь вправо от средней и, чтобы найти ее, надо за этой средней отсчитать по порядку ровно столько, сколько косточек было перемещено в предыдущий раз.
2. Сумма всех очков равна 168. Убедиться в этом можно непосредственным вычислением, перебрав все 28 косточек домино. Но это долго и скучно. Поступим иначе.
Предположим, что у нас имеется два комплекта домино. Разобьем все 56 косточек на 28 пар так, чтобы в каждую пару входили две косточки из разных комплектов, причем такие, что сумма очков на первых и вторых местах в них равна 6. Например: (3, 5) и (3, 1), (6, 4) и (0, 2), (0, 6) и (6, 0), (3, 3) и (3, 3) и т. д. Это, очевидно, можно сделать. Сумма очков в каждой паре равна 12, следовательно, сумма очков в двух комплектах равна 28 • 12 = 336. В одном же комплекте будет содержаться вдвое меньше очков, т. е. 168.
Сравните это решение с задачей в главе "Как сосчитать?" № 10.
5. Предположим, что такой квадрат сложить можно. Проведем параллельно основанию квадрата три прямые, делящие боковые стороны квадрата на четыре равные части. По условию каждая из проведенных прямых пересечет хотя бы одну косточку домино. Но над любой из прямых лежит четное число (4, 8 или 12) маленьких квадратов, равных половине косточки. Поэтому каждая прямая пересекает четное число косточек и, значит, не меньше двух. Таким образом, проведенные прямые пересекают не менее шести косточек. Если теперь аналогичным образом провести три прямые, параллельные боковым сторонам, то и они должны пересечь не менее шести косточек. Поскольку ни одна косточка не может пересекаться двумя прямыми, то в нашем квадрате должны присутствовать по крайней мере 12 косточек, что невозможно.
6. Такой квадрат сложить нельзя. Показать это можно точно так же, как и в предыдущей задаче. Необходимо провести по пяти прямых, параллельных сторонам квадрата.
7. Прямоугольник сложить можно. Одно из решений приведено на рисунке.

1. Задача решается в 24 хода следующими перемещениями:
6 в 5 2 в 4 4 в 6
4 в 6 1 в 2 2 в 4
3 в 4 3 в 1 3 в 2
5 в 3 5 в 3 5 в 3
7 в 5 7 в 5 7 в 5
8 в 7 9 в 7 6 в 7
6 в 8 8 в 9 4 в 6
4 в 6 6 в 8 5 в 4
2. Исходное положение шашек показано на рис. 1.
Первое перемещение. Слева имеем два свободных места, перекладываем туда 6-ю и 7-ю шашки. Получается расположение, как на рис. 2.
| o | ● | o | ● | o | ● | o | ● | ● | o | o | ● | o | ● | o | ● | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 8 | ||
| рис. 1 | рис. 2 | ||||||||||||||||
Второе перемещение. 3-ю и 4-ю шашки перекладываем на освободившиеся места и получаем рис. 3.
|
● |
o | o | ● | o | o | ● | ● | |
| 6 | 7 | 1 | 2 | 5 | 3 | 4 | 8 | |
| рис. 3 | ||||||||
Т р е т ь е перемещение. 7-ю и 1-ю шашки перекладываем на свободные места, получаем расположение, как на рис. 4.
| ● | ● | o | o | o | o | ● | ● | ● | ● | ● | ● | o | o | o | o | ||
| 6 | 2 | 7 | 1 | 5 | 3 | 4 | 8 | 6 | 4 | 8 | 2 | 7 | 1 | 5 | 3 | ||
| рис. 4 | рис. 5 | ||||||||||||||||
Четвертое перемещение. Наконец, перекладываем на свободные места 4-ю и 8-ю шашки и получаем требуемое расположение: идут подряд четыре черных и четыре белых шашки (рис. 5).
Из этого последнего расположения шашек, наоборот, можно перейти к исходному также четырьмя перемещениями. Решите эту обратную задачу. Теперь это нетрудно.
3. Первоначальное расположение шашек показано на рис. 1. На рис. 2 показаны последовательные перемещения шашек:
|
1) перемещаются на свободные места 8-я и 7-я шашки; |
● | o | o | ● | o | ● | o | ● | o | ● | ||||||||||||
| 8 | 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | |||||||||||||
|
2) перемещаются на свободные места 3-я и 4-я шашки; 3) перемещаются на свободные места 6-я и 9-я шашки; |
● | o | o | ● | o | ● | o | o | ● | ● | ||||||||||||
| 8 | 9 | 1 | 2 | 5 | 6 | 7 | 3 | 4 | 10 | |||||||||||||
|
4) перемещаются на свободные места 9-я и 1-я шашки; |
● | o | o | ● | ● | o | o | o | ● | ● | ||||||||||||
| 8 | 9 | 1 | 2 | 6 | 7 | 5 | 3 | 4 | 10 | |||||||||||||
|
5) наконец, перемещаются на свободные места 4-я и 10-я шашки. |
● | ● | ● | o | o | o | o | o | ● | ● | ||||||||||||
| 8 | 2 | 6 | 7 | 5 | 9 | 1 | 3 | 4 | 10 | |||||||||||||
| o | ● | o | ● | o | ● | o | ● | o | ● | ● | ● | ● | ● | ● | o | o | o | o | o | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 8 | 4 | 10 | 2 | 6 | 7 | 5 | 9 | 1 | 3 | |||
|
рис. 1 |
рис. 2 | |||||||||||||||||||||
4. Первоначальное расположение показано на рисунке задачи. Последовательные перемещения показаны на рисунке.
| ● | o | o | ● | o | ● | o | ● | o | ● | o | ● | ||
| 10 | 11 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 12 | ||
| ● | o | o | ● | o | ● | o | ● | o | o | ● | ● | ||
| 10 | 11 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 7 | 8 | 12 | ||
| ● | o | o | ● | o | ● | ● | o | o | o | ● | ● | ||
| 10 | 11 | 1 | 4 | 5 | 6 | 2 | 3 | 9 | 7 | 8 | 12 | ||
| ● | o | o | ● | ● | ● | o | o | o | o | ● | ● | ||
| 10 | 11 | 1 | 6 | 2 | 4 | 5 | 3 | 9 | 7 | 8 | 12 | ||
| ● | ● | ● | ● | o | o | o | o | o | o | ● | ● | ||
| 10 | 6 | 2 | 4 | 5 | 11 | 1 | 3 | 9 | 7 | 8 | 12 | ||
| ● | ● | ● | ● | ● | ● | o | o | o | o | o | o | ||
| 10 | 8 | 12 | 6 | 2 | 4 | 5 | 11 | 1 | 3 | 9 | 7 | ||
5. Первоначальное расположение показано на рисунке задачи. Шесть последовательных перемещений показаны на рисунке.
| ● | o | o | ● | o | ● | o | ● | o | ● | o | ● | o | ● | ||
| 10 | 11 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 14 | ||
| ● | o | o | ● | o | ● | o | ● | o | ● | o | o | ● | ● | ||
| 12 | 13 | 1 | 2 | 3 | 4 | 7 | 8 | 9 | 10 | 11 | 5 | 6 | 14 | ||
| ● | o | o | ● | o | ● | ● | o | o | ● | o | o | ● | ● | ||
| 12 | 13 | 1 | 2 | 3 | 4 | 8 | 9 | 7 | 10 | 11 | 5 | 6 | 14 | ||
| ● | o | o | ● | ● | o | o | o | ● | ● | o | o | ● | ● | ||
| 12 | 13 | 1 | 2 | 8 | 9 | 7 | 3 | 4 | 10 | 11 | 5 | 6 | 14 | ||
| ● | o | o | ● | ● | ● | ● | o | o | o | o | o | ● | ● | ||
| 12 | 13 | 1 | 2 | 4 | 10 | 8 | 9 | 7 | 3 | 11 | 5 | 6 | 14 | ||
| ● | ● | ● | ● | ● | o | o | o | o | o | o | o | ● | ● | ||
| 12 | 2 | 4 | 10 | 8 | 9 | 7 | 3 | 13 | 1 | 11 | 5 | 6 | 14 |
Нетрудно догадаться, как сделать седьмое и последнее перемещение.
6. Рисунок показывает, как решается задача.
7. Для решения задачи шашки нужно поставить так, как показано на рисунке 1.
|
● |
● |
● |
o |
o |
● |
o |
● |
o |
o |
● |
o |
● |
o |
o |
● |
● |
● |
● |
o |
o |
o |
● |
o |
рис. 1
Как же найти это решение? Поставим в ряд 24 спички (рисунок 2).
| | | | | | | | | | | | | | | | | | | | | | | |
рис. 2
Считая от 1 до 7, находим, что в первый раз придется выбросить 7-ю, 14-ю и 21-ю спички. Отбрасываем их и опять начинаем считать от 1 до 7; сначала отсчитаем три спички за 21-й, а затем возвращаемся к началу ряда, который содержит теперь только 21 спичку. Из него придется на этот раз выбросить 4-ю, 12-ю и 20-ю спички. Повторяя этот процесс, на следующем шаге мы выбросим 5-ю, 15-ю, 24-ю спички, затем 10-ю, 22-ю и, наконец, 9-ю спичку. Останется 12 спичек. Если теперь на места оставшихся спичек поставить черные шашки, а на места выброшенных — белые, то получим требуемое расположение (рисунок 1).
1. Решение приведено на рисунке.

2. Для того чтобы конь обошел все свободные 63 клетки, он должен сделать 63 хода. Заметим, что при каждом ходе конь меняет цвет поля, на котором он находился. Так что после хода с номером 63 он будет находиться на поле, цвет которого отличен от цвета исходного поля. Но по условию после этого хода конь должен вернуться на исходную клетку. Полученное противоречие доказывает, что конь не может совершить требуемое путешествие.
Точно так же можно рассуждать, если на доске стоит любое нечетное число фигур.
3. Предположим, что маршрут коня, отвечающий условию задачи, существует. Перенумеруем все 62 свободных поля шахматной доски следующим образом. Исходному полю присвоим номер 1. А все оставшиеся поля будем нумеровать 2, 3, ..., 62 в том порядке, как их проходит конь. Ввиду того, что конь при каждом ходе меняет цвет поля, все поля с нечетными номерами будут иметь один цвет и точно так же одного цвета будут все поля с четными номерами. Следовательно, свободная часть доски, состоит из 31 черного и 31 белого поля. Но это неверно, так как поля, занятые пешками, имеют один цвет, Требуемый маршрут не существует.
4. Расставим в клетках центрального квадрата буквы а, b, с, d, е, f и цифру 0 так, как это показано на рисунке.
|
a |
f |
e |
b |
|
e |
0 |
0 |
f |
|
f |
0 |
0 |
e |
|
d |
e |
f |
c |
Выпишем теперь их последовательно в порядке прохождения полей конем. Получим цепочку из 16 знаков. С любого из полей, обозначенных буквами, конь может перейти на поле, обозначенное другой буквой, только через поле, где стоит 0. Поэтому в последовательности между любыми двумя буквами разного наименования обязательно встретится 0. Заменим теперь каждую группу рядом стоящих одинаковых букв одной буквой того же наименования. После этого в последовательности останется по крайней мере 6 букв и эти буквы должны быть отделены друг от друга нулями. Ясно, что имеющихся у нас четырех нулей для этого недостаточно. Следовательно, обход невозможен.
5. Как бы жуки ни переползали, всегда останется пустая клетка. Действительно, назовем черными тех жуков, которые сначала сидели на черных клетках, а остальных назовем белыми. После того, как каждый жук переполз на соседнюю клетку, все черные жуки оказались на белых клетках. Мы имеем 13 черных жуков и только 12 белых клеток. Значит, на некоторой белой клетке встретятся по крайней мере два жука. Но тогда одна клетка доски останется пустой (ведь число клеток равно числу жуков).
Точно такой же ответ будет в случае любой квадратной доски с нечетным числом клеток. Подтвердить это можно аналогичным рассуждением.
6. Жуки могут переползти на соседние поля так, что все клетки останутся занятыми. Чтобы показать это, давайте разрежем шахматную доску на кольца (рисунок). И пусть каждый жук переползет по своему кольцу на соседнюю клетку, двигаясь по направлению движения часовой стрелки. Очевидно, при этом каждая клетка останется занятой.

7. На рисунке показана замкнутая линия, проходящая через каждую клетку доски. Если жук будет ползти по этой линии в одном направлении, то он обойдет доску так, как это требуется условием задачи.
8. Если бы это можно было сделать, то покрытым оказалось бы четное число клеток: ведь каждая кость домино покрывает в точности две клетки. Но свободная часть доски состоит из 63 клеток. Ответ: невозможно.
9. Каждая положенная на доску кость домино покрывает одно черное и одно белое поле. Поэтому, если какая-то часть доски покрыта костями домино, то она состоит из одинакового числа черных и белых полей. Но пешки, поставленные на доску, заняли два поля одного цвета; значит, в оставшейся части доски будет разное число черных и белых клеток (по всей доске 32 черных и 32 белых поля). Значит, ее нельзя покрыть костями домино.
Из приведенного рассуждения видно, что если мы поставим две пешки на любые поля одного цвета, то оставшаяся часть доски не может быть покрыта костями домино.
10. Рассмотрим замкнутую линию на рисунке ответа задачи 7. Если пешки стоят на соседних полях, то разорванная линия будет состоять из одного куска, проходящего через 62 поля, при этом цвета полей чередуются. Легко видеть, что если мы начнем класть кости домино вдоль этой линии, то закроем всю оставшуюся часть доски. Если пешки не стоят на соседних полях, то линия разорвется на два непересекающихся куска. Каждый при этом будет проходить через четное число клеток (пешки стоят на полях разных цветов). Значит, каждый кусок линии может быть закрыт костями домино.
Ответ: как бы мы ни расставляли две пешки на полях разных цветов, оставшуюся часть доски всегда можно покрыть костями домино.
11. Если мы разместим 32 шахматные фигуры на белых полях, то все белые поля будут заняты и кость домино положить будет негде (как мы уже условились, кость домино покрывает два соседних поля, одно из них белое, другое черное).
Покажем, что, как бы мы ни размещали на доске 31 фигуру, всегда найдется место для домино. Покроем шахматную доску 32 костями домино (например, вдоль линии на рисунке ответа задачи 7). Как бы мы ни расставляли теперь на доске 31 фигуру, по крайней мере на одной кости фигур стоять не будет.
Этим все и доказано.
1. Конечно, можно во всех клетках квадрата поставить число 2. Получившийся числовой квадрат будет удовлетворять условиям задачи. Но, если потребовать, чтобы среди чисел было по крайней мере одно нечетное, задача становится не такой простой.
Прежде всего, сделав несколько проб, легко убедиться, что в центре квадрата не могут стоять ни 1, ни 3. Этому факту можно дать и строгое доказательство.
Предположим, что числа расставлены так, как требуется. Прибавим друг к другу числа, стоящие на диагоналях и во втором столбце (при этом число, стоящее в центре квадрата, будет взято трижды), и вычтем из результата числа, стоящие в первой и третьей строках. Разность, как легко видеть, будет равна утроенному числу из центра квадрата. С другой стороны, сумма чисел на диагоналях, в каждом столбце и в каждой строке равняется 6; значит, разность должна равняться 6. Следовательно, в центре квадрата стоит число 2.
Далее, легко видеть, что сумма чисел равняется б только в том случае, если все они различны или все равны 2. Поэтому по крайней мере в одной из вершин квадрата должно стоять число 2. Искомые расстановки теперь легко находятся (рис. 1). Все они получаются из первой с помощью симметрий относительно диагонали (2, 2, 2), относительно второй строки и относительно второго столбца.
| 1 | 3 | 2 | 3 | 1 | 2 | 2 | 1 | 3 | 2 | 3 | 1 | |||
| 3 | 2 | 1 | 1 | 2 | 3 | 3 | 2 | 1 | 1 | 2 | 3 | |||
| 2 | 1 | 3 | 2 | 3 | 1 | 1 | 3 | 2 | 3 | 1 | 2 | |||
| рис. 1 | ||||||||||||||
Для построения нужного размещения чисел можно воспользоваться одним легко запоминающимся приемом. Расположим сначала числа так, как на рис. 2, а. Затем числа, лежащие вне квадрата ABCD, сдвигаем соответственно вниз, вверх, влево или вправо на 3 клетки так, чтобы они попали на свободные места в квадрате. Получаем в результате требуемое размещение (рис. 2, b).
| 1 | ||||||||
| 4 | 2 | 4 | 9 | 2 | ||||
| 7 | 5 | 3 | 3 | 5 | 7 | |||
| 8 | 6 | 8 | 1 | 6 | ||||
| 9 | ||||||||
|
рис. 2 a |
|
рис. 2 b |
||||||
2. Поступим так же, как в конце решения предыдущей задачи. Расставим числа, как показано на рис. 1 а, а затем сдвинем стоящие вне квадрата числа соответственно на 3 клетки влево, вправо, вниз и вверх так, чтобы они попали на свободные места в квадрате. Получим нужное размещение (рис. 1 b).
| A | 1 | B | A | B | |||||
| 1 | 2 | 1 | 3 | 2 | |||||
| 1 | 5 | 3 | 3 | 2 | 1 | ||||
| 2 | 3 | 2 | 1 | 3 | |||||
| D | 3 | C | D | C | |||||
|
рис. 1 a |
|
рис. 1 b |
|||||||
Можно также для решения этой задачи взять соответствующие кости домино (рис. 2).

Рис. 2
3. Использованный нами прием поможет и в этом случае.
Пристроим на всех сторонах квадрата из 25 клеток еще по четыре клетки (рис. 1), а затем в полученной фигуре расположим косыми рядами последовательно числа от 1 до 25.
| 1 | ||||||||
| A | 6 | 2 | B | |||||
| 11 | 7 | 3 | ||||||
| 16 | 12 | 8 | 4 | |||||
| 21 | 17 | 13 | 9 | 5 | ||||
| 22 | 18 | 14 | 10 | |||||
| 23 | 19 | 15 | ||||||
| D | 24 | 20 | C | |||||
| 25 | ||||||||
| рис. 1 | ||||||||
Затем, сдвинув все числа, стоящие вне квадрата ABCD, на 5 клеток соответственно вниз, вверх, влево и вправо, получим требуемое расположение (рис. 2).
| 11 | 24 | 7 | 20 | 3 |
| 4 | 12 | 25 | 8 | 16 |
| 17 | 5 | 13 | 21 | 9 |
| 10 | 18 | 1 | 14 | 22 |
| 23 | 6 | 19 | 2 | 15 |
| рис. 2 | ||||
4. Прием, изложенный в решениях предыдущих задач, не позволяет, как легко видеть, строить волшебные квадраты с 16 клетками, и тем не менее существует большое число расположений, удовлетворяющих условиям задачи.
Не рассматривая общего приема решения таких задач, приведем лишь два ответа к этой задаче (рисунок).
| 4 | 5 | 14 | 11 | 3 | 2 | 15 | 14 | ||
| 1 | 15 | 8 | 10 | 13 | 16 | 1 | 4 | ||
| 16 | 2 | 9 | 7 | 10 | 11 | 6 | 7 | ||
| 13 | 12 | 3 | 6 | 8 | 5 | 12 | 9 |
Простой способ, использованный нами в решениях задач 2, 3, пригоден для построения волшебных квадратов с любым нечетным количеством клеток. К сожалению, приемы построения волшебных квадратов с четным числом клеток намного более сложны.
5. Прежде всего предположим, что буквы одинаковы. Поставим одну букву в какой-нибудь клетке первой диагонали. При этом на второй диагонали окажутся запрещенными две клетки, стоящие в одном горизонтальном и вертикальном ряду с уже занятой клеткой. В одной из остальных двух клеток второй диагонали можно поставить вторую букву. Далее легко заметить, что две буквы, поставленные на диагоналях, однозначно определяют расстановку в соответствии с условиями задачи двух оставшихся букв (рисунок).
| a | |||
| a | |||
| a | |||
| a |
Итак, если фиксировать место буквы на первой диагонали, то задача имеет два решения. Но так как первую букву можно поставить в любой клетке первой диагонали, то задача имеет 2 х 4 = 8 решений. Так как четыре различных буквы можно перемещать 24 способами, то в этом случае задача имеет 8 х 24 = 192 решения.
6. Предположим, что мы расставим буквы так, Как это требуется в задаче. Поменяем местами какие-либо два столбца или две строки. При этом получится новое расположение букв, также удовлетворяющее условию задачи. Очевидно, столбцы и строки можно переставить так, что в верхней строке и крайнем левом столбце буквы разместятся в таком порядке, как показано на рис. 1.
| a | b | c | d |
| b | |||
| c | |||
| d |
рис. 1
Подобные расположения букв будем называть основными. Найдем теперь все основные расстановки букв. Легко видеть, что во второй строке буквы а, с, d можно разместить только тремя способами: (с, d, а), (d, а, с), (a, d, с). Первым двум соответствуют единственные расположения букв в третьей и четвертой строках, третьему соответствуют два расположения. Итак, имеется всего четыре основных размещения букв, представленных на рис. 2.
| a | b | c | d | a | b | c | d | a | b | c | d | a | b | c | d | |||
| b | c | d | a | b | d | a | c | b | a | d | c | b | a | d | c | |||
| c | d | a | b | c | a | d | b | c | d | a | b | c | d | b | a | |||
| d | a | b | c | d | c | b | a | d | c | b | a | d | c | a | b |
рис. 2
Из каждого основного перестановкой столбцов можно получить 24 новых размещения. А при каждом расположении столбцов перестановкой второй, третьей и четвертой строк — еще 6 новых. Очевидно, все эти расположения различны. Итак, существует
4 • 26 • 6 = 576
различных расстановок букв, удовлетворяющих условию задачи.
7. Обозначим для краткости звания офицеров буквами П, М, К, Л, а номера полков цифрами 1, 2, 3, 4. Очевидно, каждый офицер полностью характеризуется парой: (буква, цифра), Например (К, 3) — капитан из третьего полка. Задача, следовательно, сводится к тому, чтобы в 16 клетках квадрата разместить по четыре буквы П, М, К, Л и по четыре цифры 1, 2, 3, 4 так, чтобы в каждом горизонтальном и вертикальном ряду не было одинаковых букв и цифр. Кроме того, все пары (буква, цифра) должны быть различны.
Расположим сначала буквы (см. предыдущую задачу) так, как показано на рис. 1:
| П | М | К | Л |
| Л | К | М | П |
| М | П | Л | К |
| К | Л | П | М |
рис. 1
Чтобы разместить цифры, мы сначала приставим к каждой букве соответствующую ей по порядку цифру (т, е. ко всем П приставим 1, ко всем М приставим 2, ко всем К приставим 3, ко всем Л приставим 4), а затем переставим каждую цифру в клетку, симметричную относительно диагонали (П, К, Л, М ). В результате получим рис. 2. Это расположение и является ответом к задаче.
|
П,1 |
М,4 |
К,2 |
Л,3 |
|
Л,2 |
К,3 |
М,1 |
П,4 |
|
М,3 |
П,2 |
Л,4 |
К,1 |
|
К,4 |
Л,1 |
П,3 |
М,2 |
рис. 2
8. Рассмотрим квадрат из 16 клеток. Пусть его строки отвечают участникам первой команды, а столбцы — участникам второй команды.
Разместим в клетках квадрата пары цифр следующим образом. Возьмем размещение букв и цифр предыдущей задачи и заменим каждую букву соответствующей ей цифрой (П " 1, М " 2, К " 3, Л " 4). В результате получим рис. 1.
|
II I |
1 | 2 | 3 | 4 |
| 1 | 1.1 | 2.4 | 3.2 | 4.3 |
| 2 | 4.2 | 3.3 | 2.1 | 1.4 |
| 3 | 2.3 | 1.2 | 4.4 | 3.1 |
| 4 | 3.4 | 4.1 | 1.3 | 2.2 |
| рис. 1 | ||||
Положим теперь, что первая цифра в каждой клетке указывает номер тура, в котором встречаются игроки, соответствующие строке и столбцу, содержащим данную клетку. И если вторая цифра нечетная, то игрок первой команды играет белыми, а в противном случае черными фигурами. Поскольку любая цифра, стоящая на первом месте, встречается в каждой строке и в каждом столбце по одному разу, то в любом туре будут заняты все шахматисты, при этом у каждого будет определен единственный партнер.
Покажем, что такое расписание удовлетворяет условиям задачи. Так как в каждой строке и в каждом столбце на втором месте расположены числа 1, 2, 3, 4 в некотором порядке, то каждый шахматист сыграет по две партии белыми и по две партии черными фигурами. Далее, так как все пары различны, то, выбрав любые четыре пары чисел, отвечающие одному туру, т. е, имеющие на первом месте одну и ту же цифру — номер тура, мы получим на вторых местах расположенные в некотором порядке числа 1, 2, 3, 4. Это означает, что в данном туре игроки первой команды будут играть две партии белыми и две партии черными фигурами. Нагляднее это расписание игр представлено на рис. 2. Здесь цвет клетки Означает цвет фигур, которыми должен играть представитель первой команды, а цифра — номер тура, в котором встречаются соперники.
|
II
I
|
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
4 |
3 |
2 |
1 |
|
3 |
2 |
1 |
4 |
3 |
|
4 |
3 |
4 |
1 |
2 |
|
рис. 2 |
||||
Опишем некоторые способы построения латинских квадратов произвольного размера. Элементы такого квадрата размером n x n будем обозначать целыми числами.
I. Пусть р — простое число и n = р - 1. Перенумеруем строки квадрата сверху вниз и столбцы слева направо числами от 1 до n. На пересечении строки с номером а и столбца с номером b поместим остаток от деления на p числа ab. Так как номера строк и столбцов есть положительные целые числа, не делящиеся на p, то в каждой клетке квадрата будет стоять одно из чисел 1, 2, ..., n. Докажем, что в каждой строке стоят различные числа. Если в строке с номером а стоят два равных числа, скажем в столбцах с номерами Ь, с, то это означает, что числа ab, ас имеют одинаковые остатки при делении на р и, значит, их разность а(b - с) делится на р. Но оба сомножителя а и b - с отличны от нуля и по абсолютной величине меньше р. Следовательно, делимость не может иметь места, числа ab и ас имеют разные остатки при делении на р. Точно так же доказывается, что и в любом столбце квадрата стоят различные числа. Так как строки и столбцы содержат по n клеток, а всевозможных ненулевых остатков от деления на р тоже имеется n, то каждая строка и каждый столбец будут представлять собой некоторую перестановку чисел 1, 2, n.
Если построить таким способом латинский квадрат при р = 5, а затем заменить цифры 1, 2, 3, 4 буквами а, Ь, с, d соответственно, то получится второй из квадратов на рис. 2 ответ на задачу 6.
II. Пусть n — произвольное целое положительное число и k — целое число, не имеющее общих с n делителей. Поместим на пересечении строки с номером а и столбца с номером b остаток от деления на n числа ak + b. Если на пересечении столбцов с номерами b, с и строки с номером а стоят равные числа, то разность ak + b - (ak + с) = b - с должна делиться на n. Но это невозможно, так как b, с — различные целые числа, лежащие в пределах от 1 до n. Предположим, что в некотором столбце, скажем с номером b, будут стоять одинаковые числа. Если соответствующие строки имеют номера u, v, то разность uk + b - (vk + b) = (u - v)k должна делиться на n. Ввиду того, что числа k и n не имеют общих делителей, на n должно делиться число u - v. Но это невозможно.
Итак, в каждой строке и в каждом столбце будут стоять разные числа, Это означает, как и ранее, что столбцы и строки квадрата будут некоторыми перестановками чисел 0, 1, 2, ..., n - 1.
При n = 4 и k = 1 построенный таким способом квадрат совпадает с первым на рис. 2 ответа на задачу 6, если заменить цифры 0, 1, 2, 3 соответственно буквами с, d, а, b.
Выбирая по-разному число k, можно таким способом строить различные латинские квадраты.
Предположим, что n — простое нечетное число, k, l — различные числа из промежутка 0, 1, . . ., n - 1 и для каждого из них указанным выше способом построен латинский квадрат. Давайте проверим, что эти пары квадратов решают задачу, где участвуют представители п полков, имеющие n различных званий. Предположим, что при наложении квадратов в двух различных клетках окажутся одинаковые пары чисел. Если эти клетки расположены в строках с номерами а, u и столбцах с номерами b, v соответственно, то обе разности
ak + b - (uk + v) = (а - u)k + b - v,
al + b - (ul + v) = (а - u)l + b - v
должны делиться на n. Отсюда следует, что на n делится разность
(а - u)k - (а - u)l = (а - u)(k - l).
Нo это возможно только в случае а = u, а тогда на n должна делиться разность b - v. Следовательно, b = v, и получается, что клетки должны совпадать.
Пары латинских квадратов, решающие предыдущую задачу при некотором n, дают возможность составить расписание турнира с n участниками подобно тому, как это делалось в решении этой задачи. Интересно, что при n = 6 расписание турнира может быть составлено, хотя предыдущая задача неразрешима.
1. С первого взгляда кажется ясным, что паук должен пробежать потолок по диагонали СЕ и затем спуститься к мухе по ребру ЕК.
Поразмыслив, мы найдем для паука и другой путь: он может пробежать боковую стену по диагонали CF и подобраться к жертве по FK.
И, наконец, паук мог бы пойти по СА и по АК.
Параллелепипед симметричен относительно середины диагонали СК, поэтому каждый из путей CDK, СВК и СGК равен по длине одному из трех приведенных выше путей.
Какой же из них является кратчайшим?
Оказывается, что ни тот, ни другой, ни третий. Есть еще более короткие пути, займемся их разыскиванием.
Ввиду симметрии параллелепипеда можно считать, что кратчайший путь паука не заходит на боковую стену АВЕК.
Действительно (рис. 1), например, длина пути KLC равняется длине пути КМС. Поэтому можно считать, что путь пересекает одно из ребер EG, GF, FD, AD. Ввиду симметрии ребер AD и EG достаточно считать, что он пересекает EG, GF или FD.
рис. 1
Развернем параллелепипед, изображающий нашу комнату, на плоскость. Получим чертеж, представленный на рис. 2.
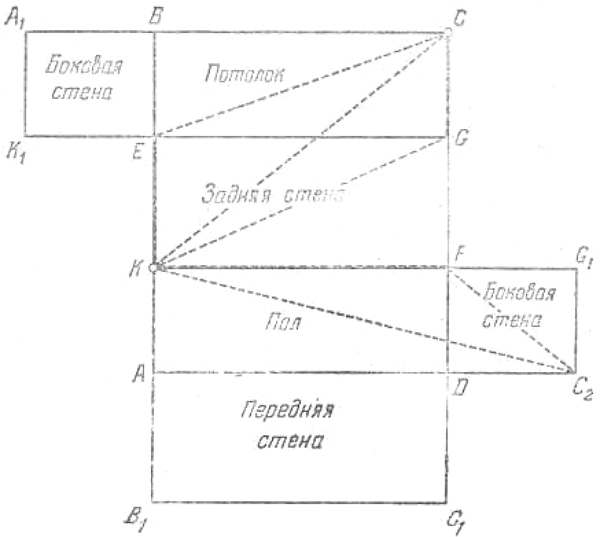
рис. 2
Паук сидит в точке С, а муха — в точке K. Теперь мы ясно видим, что пути СЕК и CGK, казавшиеся нам в неразвернутом чертеже кратчайшими, на самом деле таковыми не являются. Стоит соединить точки С и К прямой линией, чтобы получить заметно более короткий путь. Этот путь будет кратчайшим среди всех путей, пересекающих ребро EG. Аналогично, путь КС2 будет кратчайшим среди всех путей, пересекающих ребро FD (точка С2 также отвечает вершине С нашего параллелепипеда). В частности, он будет короче пути CFK.
Для того чтобы представить себе кратчайший среди путей, пересекающих ребро GF, развернем комнату, как показано на рис. 3. Мы видим, что KC3 — кратчайший из путей, пересекающих ребро GF.
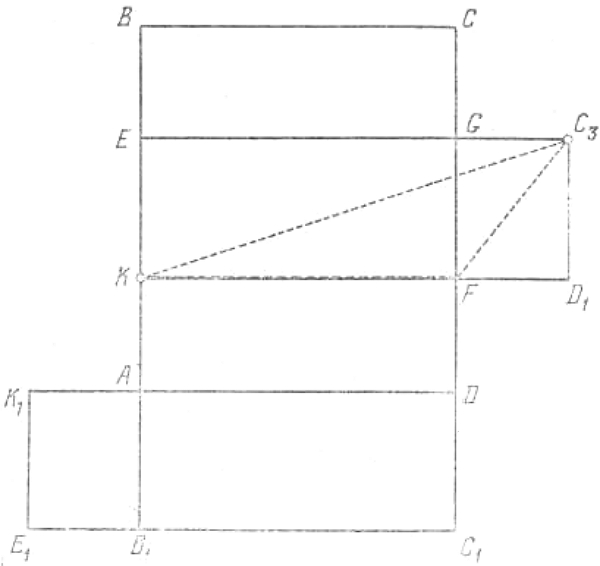
рис. 3
Остается теперь решить вопрос: какой же из этих трех путей (КС, КС2, КС3) будет самым коротким. Оказывается, что это зависит от относительных размеров комнаты в длину, ширину и высоту.
Обозначим длину комнаты AD через а, высоту АВ через b и ширину АК через с. Тогда из рис. 2 и 3 имеем
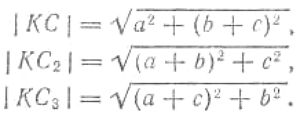
Раскрывая скобки и сравнивая между собой подкоренные выражения, мы видим, что они отличаются друг от друга лишь членами
2bс, 2аЬ, 2ас.
Деля все три произведения на 2аЬс, получим
1/a, 1/c, 1/b.
Отсюда видно, что если
а > b, а > с,
то кратчайшим путем будет путь KС; если
с > а, с > b,
то кратчайший путь KC2; если же
b > а, b > с,
то кратчайший путь KС3.
Мы видим, что кратчайший путь паука должен пересекать самое длинное из ребер
EG, GF, FD.
Задача о пауке и мухе оказалась гораздо сложнее, чем можно было думать с первого взгляда.
3. Имеется только две нечетных местности D и Е. Все остальные местности четные. Из общих рассуждений перед условием задачи следует, что она разрешима.
Кроме того, мы знаем, что обход должен начаться из нечетной местности D или Е.
Искомый обход мостов может быть сделан так!
EaFbBcFdAeFjCgAhCiDkAmEnApBqElD,
или в обратном порядке. Маленькие буквы среди больших показывают, какие именно переходятся мосты.
4. Исследуя разрешимость задачи, сразу видим, что Финляндия, Испания и Дания имеют нечетное число границ с соседними государствами, т. е. число нечетных местностей более двух. А следовательно, путешествие, которое предполагает совершить контрабандист, невозможно.
5. См. рисунок.
6. Изобразим каждого рабочего и каждый станок на листе бумаги в виде точки. Всего получится 20 различных точек. Проведем теперь из каждой точки, изображающей рабочего, две линии к точкам, изображающим станки, на которых этот рабочий умеет работать. Мы получим сеть, состоящую из 20 точек и 20 линий, причем из каждой точки, вне зависимости от того, соответствует она рабочему или станку, выходят две линии.
Получившаяся сеть распадается на несколько кусков таких, что в пределах одного куска можно пройти по линиям сети от каждой точки до любой другой. Если же точки принадлежат разным кускам, то не существует пути, соединяющего их.
Так как в каждом куске сети все вершины четные, то его можно вычертить одним росчерком. Расставим на каждой линии сети стрелочки в соответствии с направлением вычерчивания. Тогда из каждой точки сети будет выходить единственная линия.
Линия, выходящая из точки, изображающей рабочего, будет входить в точку, изображающую станок, на котором этот рабочий будет работать.
Утверждение остается верным, если число 10 в условии задачи заменить любым другим целым числом, не меньшим 2. Решение остается тем же самым.