Всё, что есть у меня - Ваше
Игры с числами и предметами
Знакомство с удивительным миром математики начинается в дошкольном возрасте. Дети с интересом и желанием знакомятся с цифрами, учатся ими оперировать, сравнивают предметы по величине, изучают геометрические фигуры и осваивают навык ориентировки в пространстве и времени. Математика дает огромные возможности для развития мышления, логики и внимания.
Для успешного овладения знаниями по разделам формированию элементарных математических представлений (ФЭМП) большая роль отводится дидактическим играм. Игра – ведущий вид деятельности детей, только в игре ребенок ненавязчиво усваивает и успешно закрепляет знания.
Каждая из игр по ФЭМП решает конкретную задачу совершенствования математических (количественных, пространственных, временных) представлений детей.
Дидактические игры включаются непосредственно в содержание занятий по ФЭМП как одно из средств реализации программных задач, а также для индивидуальной работы по закреплению знаний детей во второй половине дня. Дидактические игры в структуре занятия по ФЭМП определяются возрастом детей, целью, назначением, содержанием занятия.
Математические навыки
важны для нормального развития
умственных способностей малыша. В
дошкольный период у детей закладывается
фундамент для развития его умственной
деятельности. Из многообразия игр для
усвоения знаний по математике наиболее
широко применяются дидактические игры.
Они развивают:
• Сенсорные способности;
• Наблюдательность;
• Внимание;
• Мышление;
• Воображение;
• Содействуют усвоению математических
понятий;
• Учат соотносить число и количество;
• Обучают умению ориентироваться в
пространстве.
Для проведения таких игр обязательно потребуются разные предметы и наглядные материалы. Такие игры для дошкольников наиболее рекомендуется проводить в увлекательной форме.
Для формирования математических навыков у ребенка огромную помощь ему окажут родители. Уютная обстановка дома значительно раскрепостит и расслабит малыша, поможет закрепить знания, приобретенные в детском саду.
Дидактические игры с родителями позволяют выбрать темп и сложность игр в зависимости от возраста малыша и его индивидуальных особенностей, а также помогут как можно лучше узнать своего кроху и сблизиться с ним.

Пользуясь тремя пятерками и какими угодно знаками математических действий, написать выражение, равное единице. Если вы никогда не пробовали решать подобные задачи, то вам немало придется подумать, прежде чем вы нападете на правильное решение.
Вот одно решение предлагаемой задачи: 1 = (5/5)5.
Попробуйте найти другие решения.
Записать двойку тремя пятерками
Как записать двойку тремя пятерками?
Записать четыре тремя пятерками
Как записать четыре тремя пятерками?
Записать пять тремя пятерками
Как записать пять тремя пятерками?
Записать нуль тремя пятерками
Как записать нуль тремя пятерками?
Записать 31 пятью тройками
Как записать 31 пятью тройками?
В автобусе вам попался билет с номером 524127. Попробуйте, не меняя порядка цифр, расставить между ними знаки математических действий так, чтобы в итоге получилось 100.
Эта занятная игра может скрасить вам время длительной поездки, если вы попытаетесь получить 100 подобным же образом из номера попавшегося вам билета. Если вы едете не одни, то можно устроить маленькое соревнование: кто быстрее получит 100 из цифр своего билета.
Двое поочередно называют произвольные числа, не превышающие 10. Эти числа складываются одно за другим, и выигрывает тот, кто первый достигнет ста.
Если первый скажет, например, «7», а второй «10», получится «17»; затем первый говорит, например, «5», получится «22»; второй говорит «8», получится «30» и т. д. Победителем будет тот, кто первый получит «100».
Как сделать так, чтобы наверняка первым сказать «сто»?
Предыдущую задачу можно предложить и в таком общем виде. Двое называют поочередно произвольные числа, не превышающие, однако, какого-нибудь условленного предела. Эти числа складываются одно за другим, и выигрывает тот, кто первый достигает какого-нибудь заранее назначенного числа.
Сделать так, чтобы первым прийти к этому назначенному числу.
Десять спичек положены в один ряд (рисунок). Требуется распределить их попарно, всего в 5 пар, перекладывая по одной спичке через две (например, первую переложить к четвертой).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||
Собрать в группы по 3
Пятнадцать спичек расположены в ряд. Требуется собрать их в 5 кучек по 3 спички, перекладывая их по одной и каждый раз перескакивая при этом через 3 спички.
Возьмем 8 деревянных или из толстого картона кружков уменьшающегося диаметра и 3 вертикально укрепленные на подставках палочки (стержня). Кружки снабжены в центре отверстиями, и их накладывают, начиная с наибольшего, на одну из палочек А. Это и есть детская пирамида в 8 этажей (рисунок, вверху).
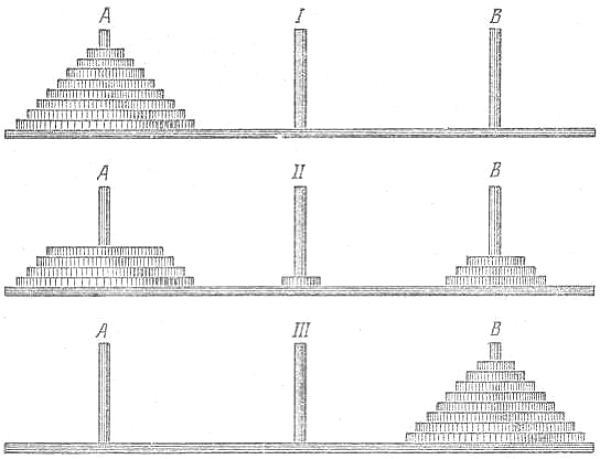
Требуется эту пирамиду с палочки А перенести на палочку В, пользуясь третьей палочкой (I, II и III на рисунке) как вспомогательной и соблюдая следующие условия:
1) не переносить за один раз более одного кружка,
2) класть снятый кружок или на ту палочку, которая свободна, или накладывать его на кружок большего диаметра.
Надевать на какую-либо из палочек больший кружок поверх меньшего нельзя.
Легенда. Если выше вместо 8 кружков возьмем 64 кружка, то получим задачу, связанную с древнеиндийской легендой. Легенда эта гласит, будто в городе Бенаресе, под куполом главного храма, в том месте, где находится середина Земли, бог Брама поставил вертикально на бронзовой площадке три алмазные палочки, каждая длиною в локоть и толщиною в корпус пчелы. При сотворении мира на одну из этих палочек были надеты 64 кружка из чистого золота с отверстиями посередине — так, что они образовали род усеченного конуса, так как диаметры их шли в возрастающем порядке, начиная сверху. Жрецы, сменяемые один другим, днем и ночью без устали трудятся над перенесением этой колонны кружков с первой палочки на третью, пользуясь второй как вспомогательной, причем они обязаны соблюдать условия, т. е. 1) не переносить за один раз более одного кружка и 2) класть снятый кружок или на свободную в этот момент палочку, или накладывать его на кружок только большего диаметра. Когда, соблюдая все эти условия, жрецы перенесут все 64 кружка с первой палочки на третью, наступит конец мира...
Попробуйте со своим товарищем сыграть в следующую игру. Разложите на столе три кучки спичек. Например, в 12, 10 и 7 спичек. Игра заключается в том, чтобы поочередно брать из кучек некоторое, какое вам захочется, количество спичек, но каждый раз только из одной кучки. Можно взять и сразу целую кучку. Выигрывает тот, кто последним возьмёт спички. Давайте для примера разыграем партию. Одного игрока обозначим А, другого Б.
| Исходное положение | 12, | 10, | 7 | |||
| После | хода | А | 12, | 10, | 6 | |
| » | » | Б | 12, | 7, | 6 | |
| » | » | А | 1, | 7, | 6 | |
| » | » | Б | 1, | 5, | 6 | |
| » | » | А | 1, | 5, | 4 | |
| » | » | Б | 1, | 3, | 4 | |
| » | » | А | 1, | 3, | 2 | |
| » | » | Б | 1, | 2, | 2 | |
| » | » | А | 0, | 2, | 2 | |
| » | » | Б | 0, | 1, | 2 | |
| » | » | А | 0, | 1, | 1 | |
| » | » | Б | 0, | 0, | 1 | |
Последним ходом игрок А выигрывает.
Вопрос состоит в следующем: может ли А играть так, чтобы всегда выигрывать?