Всё, что есть у меня - Ваше

Геометрические софизмы и парадоксы
 Парадоксы
можно найти везде, от экологии до
геометрии и от логики до химии. Даже
компьютер, на котором вы читаете статью,
полон парадоксов. Перед вами — десять
объяснений довольно увлекательных
парадоксов. Некоторые из них настолько
странные, что мы просто не можем
полностью понять, в чём же суть.
Парадоксы
можно найти везде, от экологии до
геометрии и от логики до химии. Даже
компьютер, на котором вы читаете статью,
полон парадоксов. Перед вами — десять
объяснений довольно увлекательных
парадоксов. Некоторые из них настолько
странные, что мы просто не можем
полностью понять, в чём же суть.
История математики полна
интересных и неожиданных софизмов. И
зачастую именно их разрешение служило
толчком к новым открытиям, из которых, в
свою очередь, вырастали новые софизмы и
парадоксы.
Необходимо различать между собой
парадоксы и софизмы. Софизм (от греч.
sophisma – уловка, выдумка, головоломка,
ухищрение, выдумка) — ложное
умозаключение, которое, тем не менее,
при поверхностном рассмотрении кажется
правильным. Софизм - формально кажущееся
правильным, но по существу ложное
умозаключение, основанное на
преднамеренно неправильном подборе
исходных положений (словарь Ожегова).
Парадокс (греч. "пара" - "против", "докса"
- "мнение") – это нечто необычное и
удивительное, то, что расходится с
привычными ожиданиями, здравым смыслом и
жизненным опытом.
Парадокс близок софизму. С софизмом их
различает то, что парадокс - не
преднамеренно полученный противоречивый
результат. Парадокс - странное,
расходящееся с общепринятым мнением,
высказывание, а также мнение,
противоречащее (иногда только на первый
взгляд) здравому смыслу. Математический
парадокс – высказывание, которое может
быть доказано и как истинна, и как ложь.

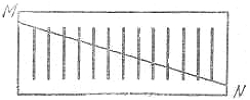
Начертите на прямоугольном куске картона 13 одинаковых палочек на равном расстоянии друг от друга, так, как показано на рис. 1 (можете наклеить на картон или плотную бумагу рис. 47, вырезав его со вспомогательной страницы). Теперь разрежьте прямоугольник по прямой MN, проходящей через верхний конец первой палочки и через нижний конец последней.
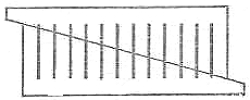
Если затем вы сдвинете обе половины так, как показано на рис. 2, то заметите любопытное явление: вместо 13 палочек перед вами окажется всего 12! Одна палочка исчезла бесследно.
 |
 |
|
| рис. 1 | рис. 2 |
Куда же она девалась?
Если вы сопоставите длины палочек на первом и втором рисунках, то обнаружите, что палочки на втором рисунке на 1/12 длиннее палочек первого рисунка. Исчезнувшая 13-я палочка улетучилась не бесследно: она словно растворилась в 12 остальных, удлинив каждую из них на 1/12 своей длины. Геометрическую причину этого понять очень легко. Прямая MN и та прямая, которая проходит через верхние концы всех палочек, образуют угол, стороны которого пересечены рядом параллельных прямых. Из подобия треугольников следует, что прямая MN отсекает от второй палочки 1/12 ее длины, от третьей 2/12, от четвертой 3/12 и т. д. Когда же мы сдвигаем обе части картона, то приставляем отсеченный отрезок каждой палочки (начиная со второй) к нижней части предыдущей. А так как каждый отсеченный отрезок больше предыдущего на 1/12, то каждая палочка должна удлиниться на 1/12 своей длины. На глаз это удлинение незаметно, так что исчезновение 13-й палочки на первый взгляд представляется довольно загадочным.
 |
 |
|
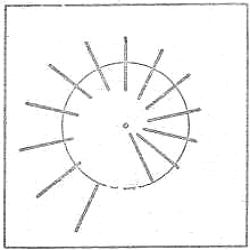
| рис. 3 | рис. 4 |
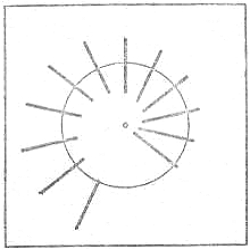
Чтобы усилить эффект, можно расположить палочки по кругу, как показано на рис. 3. Если этот рисунок, специально повторенный на вспомогательной странице, вырезать оттуда, наклеить его на картон или плотную бумагу, вырезать внутренний круг и укрепить его в центре так, чтобы он мог вращаться, то, повернув круг на небольшой угол, мы опять увидим, что одна палочка исчезла (рис. 4).
На только что рассмотренном принципе основана остроумная игрушка-задача, изображенная на рис. 5 и рис. 6 на вспомогательной странице.
 |
 |
|
|
рис. 5 |
|
рис. 6 |
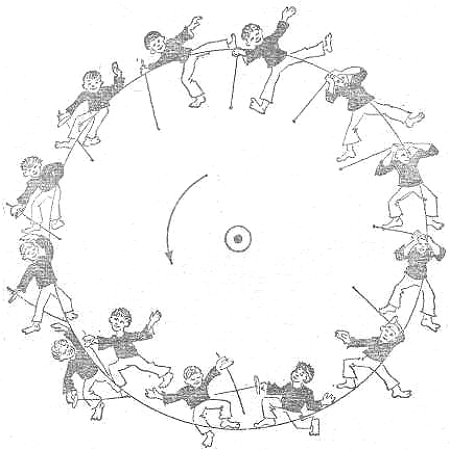
Вы видите арену цирка, по краю которой художник разместил 13 клоунов в весьма воинственных позах. Наклейте рисунок 5, специально повторенный на вспомогательной странице, на лист плотной бумаги. Вырежьте внутренний круг так, чтобы он мог вращаться вокруг своего центра. И вот, слегка повернув этот круг, вы уничтожаете одного клоуна (рис. 6); вместо прежних 13 перед вами уже всего, 12 артистов веселого жанра. Тот клоун, который находился внутри круга и так воинственно наступал на своего собрата, бесследно улетучился!..
Исчезновение клоуна заставило бы вас долго ломать голову, если бы вы не познакомились с рассмотренными выше схематическими примерами. А теперь дело ясно: он «растворился» в дюжине своих собратьев по профессии, как раньше «растворилась» у нас простая палочка.
Надо отдать справедливость художнику: немало потребовалось остроумия и терпения, чтобы достичь такого эффекта!
Вспомогательная страница
Распечатайте и отрежьте эту страничку по пунктирной линии и наклейте ее пустой стороной на картон или плотную бумагу. Вырежьте сделанные на этой странички рисунки. Затем вырежьте из верхнего и нижнего рисунка внутренний круг (осторожно делая разрез бритвой по линии окружности, на которую «нанизаны» фигурки клоунов или, соответственно, «нанизаны» палочки), а средний рисунок разрежьте по линии MN. Вы получите три забавные игрушки, описания которых вы найдете на основной странице.
|
|
|
|
|
|
|
|
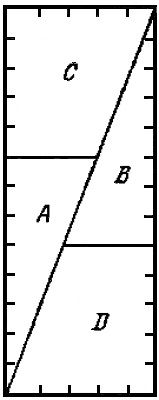
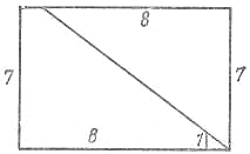
В дне деревянного судна во время плавания случилась прямоугольная пробоина в 13 см длины и 5 см ширины, т. е. площадь пробоины оказалась равной 13 см х 5 см = 65 см2. Судовой плотник взял квадратную дощечку со стороной квадрата 8 см (т. е. площадь квадрата равнялась 64 см2), разрезал ее прямыми линиями на четыре части А, В, С, D так, как это показано на рис. 1, а затем сложил их так, что получился прямоугольник, как раз соответствующий пробоине (рис. 2). Этим прямоугольником он и заделал пробоину. Вышло таким образом, что плотник сумел квадрат в 64 см2 обратить в прямоугольник с площадью 65 см2.
Как это могло случиться?
 |
 |
|
| рис. 1 | рис. 2 |
Вот еще один «фокус», который можно сделать с квадратом.
 |
 |
|
|
Рис. 1 |
|
Рис. 2 |
Возьмем квадрат со стороной 8 см и, следовательно, с площадью 64 см2, Разрежем его на три части так, как показано на рисунке a. Затем переложим эти части так, как показано на рисунке b. Получается прямоугольник, площадь которого «легко вычислить»:
7 см х 9 см = 63 см2.
В чем же дело?
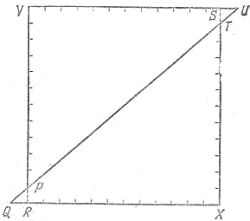
Построим прямоугольник со сторонами 11 см и 13 см. Рассечем его диагональю (рис. 1) и сдвинем затем полученные треугольники по их общей гипотенузе в положение, показанное на рис. 2. Эта последняя фигура по виду состоит из квадрата VRXS со сторонами 12 см, т. е. площадью 122 см2 = 144 см2, и двух треугольников PQR и STU, каждый площадью 0,5 см2.
Следовательно, площадь всей фигуры на рис. 2 равна 144 см2 + 2٠0,5 см2 = 145 см2.
Но как же это получилось, если площадь исходного прямоугольника равна только 13 см х 11 см = 143 см2?
|
|
 |
|
| Рис. 1 | Рис. 2 |
Вообразим, что земной шар обтянут по экватору обручем и что подобным же образом обтянут и апельсин по его большому кругу. Далее, вообразим, что окружность каждого обруча удлинилась на 1 м. Тогда, разумеется, обручи отстанут от поверхности тел, которые они раньше стягивали, и образуется некоторый зазор.
Спрашивается, в каком случае этот зазор будет больше — у земного шара или у апельсина?