Всё, что есть у меня - Ваше
Считать, вычислять и измерять
В нашей повседневной жизни мы постоянно сталкиваемся с числами: чтобы определить количество, указать время, цену, номер документа и т. д. Какими были первые числа? Какими числами пользовались майя?
Каким было первое арифметическое действие? Что такое алгоритм? Погрузись в мир цифр и открой важность чисел и действий.
Числа - это выражение определенного количества. В течение тысячелетий люди использовали пальцы рук для выражения чисел. Так один предмет они показывали одним пальцем, а три - тремя.
С помощью руки они могли показать до пяти единиц. Для выражения большего количества они использовали обе руки, а в некоторых случаях и ноги. Так, чтобы сказать шесть, они показывали одну руку и палец, чтобы сказать десять - обе руки, а чтобы сказать двадцать - обе руки и две ноги.
В настоящее время наше общество постоянно пользуется числами. Мы их используем, чтобы измерить время, купить и продать, позвонить, посмотреть телевизор, вести автомобиль. К тому же у каждого человека есть различные числа, идентифицирующие его: в удостоверении личности, в паспорте, банковском счете, кредитной карточке и т. д.
Больше того, сегодня в компьютерном мире вся информация предается посредством числовых кодов.
Мы встречаемся с числами на каждом шагу и настолько с этим свыклись, что почти не отдаем себе отчета, насколько важны они в нашей жизни. Числа составляют часть человеческого мышления. На протяжении истории каждый народ писал числа, считал и вычислял в самых различных формах.
Числа имеют две основные функции: первая - определение порядка, занимаемого элементом в ряду или в множестве элементов, и вторая — выражение количества элементов, образующих ряд или множество. Таким образом числа служат для упорядочения и определения, а также для счета и измерения. Когда их используют для счета и измерения, числа выражают количества или величины и могут добавляться одни к другим, то есть с ними можно производить действия. Сложение, вычитание, умножение, деление и возведение в степень являются арифметическими или математическими действиями.
Наука математика изучает главным образом числа и величины и действия с числами и величинами.
Но математика также изучает, помимо чисел, отношения и характеристики элементов множества и их общие и отличительные черты, форму и объем предметов и способ решения задач с помощью действий. Поэтому в математике существуют различные разделы: арифметика, геометрия, логика и другие.
Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. Хотя эти две культуры находились очень далеко одна от другой, их числовые системы очень похожи, как будто представляют один метод: использование засечек на дереве или камне для записи прошедших дней.
Египетские жрецы писали на папирусе, изготовленном из стеблей определенных сортов тростника, а в Месопотамии - на мягкой глине. Конечно, конкретные формы их цифр были различны, но и в той, и в другой культуре использовали простые черточки для единиц и другие метки для десятков и более высоких порядков. Кроме того, в обеих системах писали желаемую цифру, повторяя черточки и метки необходимое число раз.
 |
 |
Первые образцы письма появились примерно к третьему тысячелетию до рождества Христова и характеризуются использованием стилизованных символов для представления определенных объектов и идей. Постепенно эти знаки приняли более сложные формы.
В Месопотамии знак означал единицу и мог повторяться девять раз для изображения чисел от 1 до 9.
Знак означал число 10 и мог в сочетании с единицами изображать числа от 11 до 59.
Для изображения числа 60 использовали знак единицы, но в другом положении. Для цифр более 70 использовали знаки, упоминаемые выше, в различных комбинациях.
В старых вавилонских текстах, датируемых 1700 годом до н. э., не встречается никакого специального знака, обозначающего ноль, для его обозначения там просто оставляли пустое место, более или менее выделенное.
|
Египтяне писали иероглифами, то есть использовали рисунки для отображения какой-либо идеи или объекта. Эти рисунки изображали элементы флоры и фауны реки Нил и домашнюю утварь. Цифры они также писали иероглифами. У египтян были знаки для обозначения чисел от 1 до 10 и специальный иероглиф для обозначения десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов и десятков миллионов. |
|
|
|
|
 |
|
|
Древние римляне изобрели систему исчисления, основанную на использовании букв для отображения цифр. Они использовали в своей системе следующие буквы: I. V. L. С. D. М.Каждая буква имела различное значение, каждая цифра соответствовала номеру положения буквы. Для того чтобы прочесть римскую цифру, следует следовать пяти основным правилам: 1. Буквы пишутся слева направо, начиная с самого большого значения. Например, XV (15), DLV (555), MCLI (1151).2. Буквы I. X. С. и М могут повторяться до трех раз подряд, например II (2), XXX (30), СС (200), МССХХХ (1230).3. Буквы V. L. D. не могут повторяться.4. Цифры 4, 9, 40, 90 и 900 следует писать, комбинируя буквы: IV (4), IX (9), XL (40), ХС (90), CD (400), СМ (900). Например, 48 следует писать XLVIII, 449 - CDXUX. Обрати внимание, что значение левой буквы уменьшает значение правой.5. Горизонтальная линия над буквой увеличивает ее значение в 1000 раз. Например, V означает 5000, С III 103000 и IXDL 9550. |
|
 |
|
В Центральной Америке в первом тысячелетии нашей эры майя писали любое число, используя только три знака: точку, линию и эллипс.
Точка имела значение единицы, линия означала пять. Комбинация точек и линий служила для написания любого числа до девятнадцати. Эллипс под любым из этих чисел увеличивал его в 20 раз.
Цивилизация ацтеков пользовалась системой исчисления, состоящей только из 4 знаков:
- точка или кружок для обозначения единицы (1);
- буква «
h» для двадцати (20);- перо для цифры 400 (20 x 20);
- мешок, наполненный зерном, для 8.000 (20 x 20 x 20).
Из-за использования малого числа знаков для написания цифры приходилось повторять много раз один и тот же знак, образуя длинный ряд символов. В документах ацтекских чиновников встречаются счета, в которых указываются результаты описи и подсчетов податей, получаемых ацтеками от покоренных городов.
В этих документах можно увидеть длинные ряды знаков, похожие на настоящие иероглифы.
Происхождение китайской системы счисления более древнее и определяется между 1500 и 1200 годами до нашей эры.
В конце XIX века крестьяне, возделывающие свои поля, нашли множество черепашьих панцирей и костей животных, исписанных знаками древней китайской системы исчисления. Крестьяне, не знавшие важности этих рисунков, продали эти кости аптекарю, решившему, что они принадлежали дракону и имеют целебные свойства.
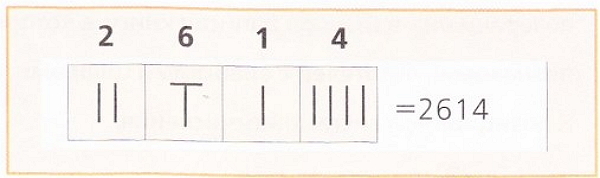
Много лет спустя в другом регионе Китая появилась новая система исчисления. Потребности торговли, управления и науки потребовали развития нового способа написания цифр. Палочками из слоновой кости или бамбука они обозначали цифры от единицы до девяти. Цифры от единицы до пяти они обозначали количеством палочек в зависимости от номера. Так, две палочки соответствовали номеру 2. Чтобы указать цифры от шести до девяти, одна горизонтальная палочка помещалась в верхней части цифры.
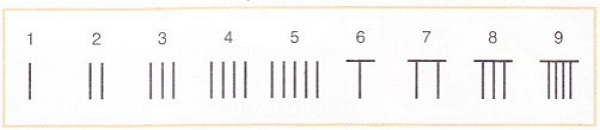
Новая система исчисления была отличительной и позиционной: каждая цифра имела определенное значение согласно месту, занимаемому в ряду, выражавшем число.
Например, номер 2614 изображали следующим образом: две вертикальных палочки, две палочки в форме «Т», одна вертикальная палочка и четыре вертикальные палочки.
Цифры, или символы наших чисел, имеют арабское происхождение, хотя они были заимствованы арабской культурой в Индии.
Промежуток между VIII и XIII веками стал одним из самых блестящих периодов в истории науки в мусульманском мире.
Мусульмане имели тесные связи как с азиатской, так и европейской культурами, и они смогли извлечь из них все самое выдающееся. В Индии они заимствовали систему исчисления и некоторые математические методы.
Современные цифры (1, 2, 3, 4, ...) не совсем точно воспроизводят индийские, поскольку арабы их слегка видоизменили, приспосабливая к своему письму. Но исходя из их влияния и авторитета их культуры, современные числовые символы называют арабскими цифрами.
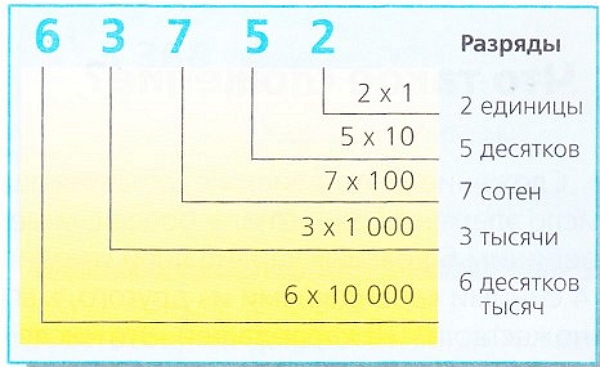
Наша система исчисления имеет три основных характеристики: она позиционная, аддитивная и десятичная.
- Позиционная, поскольку каждая цифра имеет определенное значение согласно месту, занимаемому в ряду, выражающем число: 2 означает две единицы в числе 52 и двадцать единиц в числе 25.
- Аддитивная, или слагаемая, поскольку значение одного числа равно сумме значений цифр, образующих его. Так, значение 52 равно сумме 50+2.
- Десятичная, поскольку каждый раз, когда одна цифра смещается на одно место влево в написании числа, его значение увеличивается в десять раз. Так, число 2, имеющее значение две единицы, превращается в двадцать единиц в числе 26, поскольку перемещается на одно место влево.
Первыми арифметическими действиями были сложение и вычитание. Этими действиями пользовались постоянно в каждодневной жизни. Так добавляли или отнимали определенное количество объектов: «имели 30 овец плюс четыре родились, получилось 34» или «8 коз минус одна исчезнувшая - получается 7». Для выполнения подобных действий были изобретены простые инструменты, позволяющие складывать и отнимать большие числа. В Европе и Азии использовали счеты, а в Америке инки использовали кипу, делая узелки на разноцветных веревках, которые потом связывали.
Сложение - это действие, соединяющее в одно число элементы одного или более слагаемых. Если мы соединим б красных карандашей из одного пенала с 4 синими карандашами из другого, мы получим множество из 10 карандашей. Это число, соединившее два предыдущих, и есть сумма слагаемых. Величины, входящие в сумму, могут называться одним общим термином. Например, если мы складываем 2 груши и 9 яблок, то в результате мы получаем не груши и не яблоки, а фрукты. Слагаемые, получающие одно название, называются однородными (гомогенными).
Метод, используемый нами сегодня для сложения, в основном тот же, что и много лет назад. Чтобы получить таблицу сложения, следует начертить сетку с номерами от 0 до 9. В этой таблице можно получить сумму двух номеров. Для этого следует искать результат, следуя по ряду или колонке одного из слагаемых. Результат находится в ячейке пересечения с рядом или колонкой другого слагаемого.
Вычитание - это действие, имеющее целью найти разницу между большим количеством, называемым уменьшаемым, и меньшим или равным количеством, называемым вычитаемым. Результатом этого действия является остаток, или разность. Тогда как при сложении одно количество прибавляется к другому, при вычитании одно количество отнимается от другого. Поэтому можно сказать, что вычитание является действием, обратным сложению.
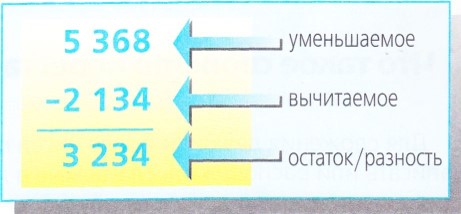
Для сложения и вычитания китайцы использовали таблицы с колонками.
В каждую колонку они вносили цифры, изображенные в виде палочек, соответствующие одному и тому же позиционному значению.
Китайское сложение
Например, сложение 7 + 8 было бы выражено так: первый и второй ряды представляли 7 и 8 соответственно, тогда как третий ряд отражал их сумму 15.
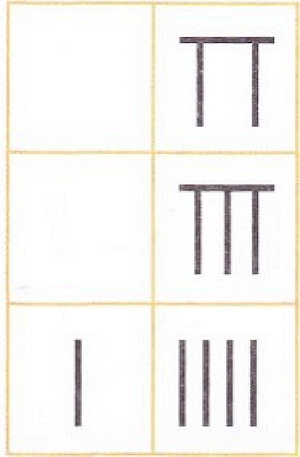
Китайское вычитание
При вычитании они использовали очень похожую систему. Например, вычитание 15 - 8 было бы отображено следующим образом: в первом и втором рядах были вписаны 15 и 8 соответственно, а в третьем ряду результат - остаток 7.
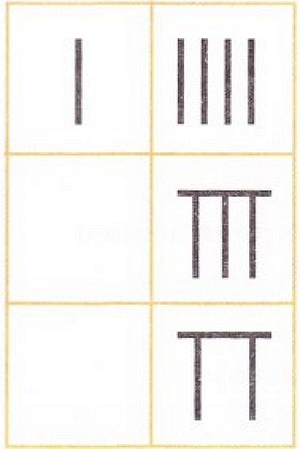
Для сложения двух или более чисел можно записать или расположить слагаемые в любом порядке, результат, или сумма, будет одним и тем же. Так 3 + 9 + 6 в результате дают ту же сумму, что 9 + 6 + 3 и 6 + 3 + 9 или 9 + 6 + 3. Сумма во всех случаях будет одна и та же: 18. Когда при арифметическом действии мы можем изменить порядок его членов и результат не меняется, то мы говорим, что это действие обладает свойством перестановки. Сложение и умножение имеют это свойство.
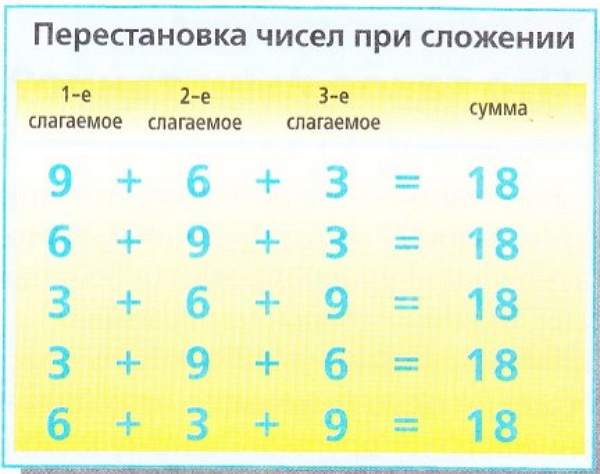
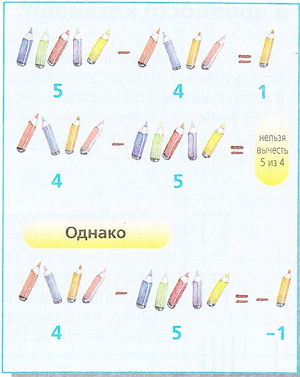
Когда мы меняем порядок чисел при вычитании, то это возможно лишь при условии использования отрицательных чисел, то есть меньше нуля.
Приведем пример: из количества в 8 карандашей можно вычесть бив результате получить 2 карандаша. Но из количества в б карандашей мы не можем вычесть 8, так как результат будет меньше нуля, то есть меньше, чем ничего.
Однако математики используют для обозначения величин менее нуля знак минус. Поэтому отрицательным числом -1 можно выразить результат вычитания 4 - 5.
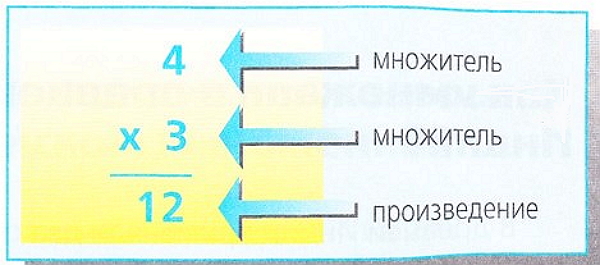
Умножение - это математическое действие, имеющее целью увеличить определенное число во столько раз, во сколько указывает другое число. Оба эти числа называются при умножении множителями, а результат произведением.
Так, умножить 3 x 4 означает увеличить 3 в 4 раза, то есть 3 + 3 + 3 + 3 = 12.
При умножении можно использовать перестановку, поэтому можно сказать, что 5 х б = 6 х 5.
Умножение можно изобразить графически с помощью отрезков прямой. Для этого вычерчиваем прямоугольник, чье основание составляет отрезок прямой, представляющий умножаемое. Например, чтобы представить умножение 6 x 3, основанием прямоугольника сделаем отрезок прямой, равный б, а высотой 3. Образовавшийся прямоугольник будет состоять из трех горизонтальных рядов, каждый из которых в свою очередь из б квадратов, то есть всего получится 18. Посмотри, как совершается действие:
6
x 3 = б + б + б = 18.
|
В древней Индии применяли два способа умножения: сетки и галеры. На первый взгляд они кажутся очень сложными, но если ты будешь следовать шаг за шагом в предлагаемых упражнениях, то увидишь, что это довольно просто. |
|
|
|
|
Посмотри, как из результатов сложения цифр по диагоналям (они выделены желтым фоном) составляется число 2 355 315,
которое и является произведением чисел 6827 и 345.
 |
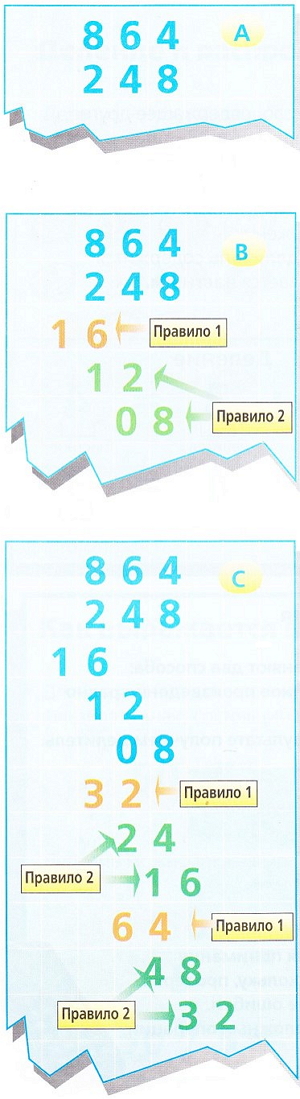Для умножения, например, 864 на 248 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец. Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 2 x 8, 2 x 6 и 2 x 4. Полученные произведения пишем в сетку (В), имея в виду следующие правила:
Правило 1. Единицы первого произведения следует писать в той же колонке, что и множимое, то есть в данном случае под 2.
Правило 2. Последующие произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения.
Теперь повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С). Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат (D). |
|
|
При умножении мы получаем произведение, то есть число, содержащее другое, повторенное определенное количество раз. Когда мы говорим, что 12 - это произведение 3 x 4, то подразумеваем, что оно содержит 4 раза 3(3 + 3 + 3 + 3) или 3 раза 4(4 + 4 + 4). В данном примере 3 и 4 являются множителями.
Деление позволяет определить один из множителей, зная другой. Поэтому мы говорим, что деление является действием, обратным умножению.
При делении определяют, сколько раз одно число или делитель содержится в другом, называемом делимым. Результат деления называется частным.
Деление - это действие, совершаемое, когда мы хотим что-то распределить. Если следует разделить 20 монет между 5 людьми, то число монет, соответствующее каждому из пятерых, и является результатом деления.
Деление представляет собой действие, используемое для решения арифметических задач, когда надо найти одну из частей продукта и распределить (разделить) элементы одного множества.
Действие возведения в степень состоит в том, что одно число умножается на самого себя несколько раз. Число, умножающееся на самого себя, называется основанием, а число раз умножения называется показателем. Результат умножения основания столько раз, сколько указывает показатель, называется возведением в степень.
Так, 9 - это 3 во второй степени, поскольку 3 x 3 = 9.
Возведение в степень 2 какого-либо числа указывает на то, что мы делаем его множителем два раза, и эта степень называется квадратной.
Так 52 = 5 x 5 = 25.
Возведение в степень 3 любого числа означает, что мы делаем его множителем три раза, и эта степень называется кубической.
Так 23 = 2 x 2 x 2 = 8.
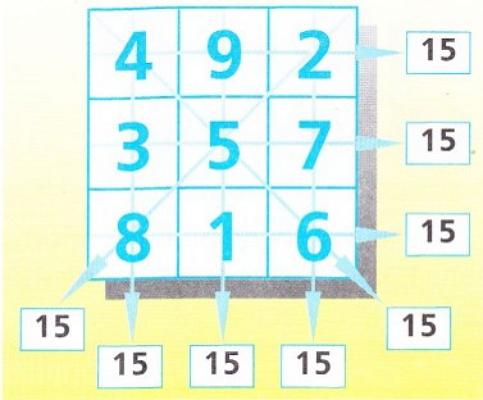
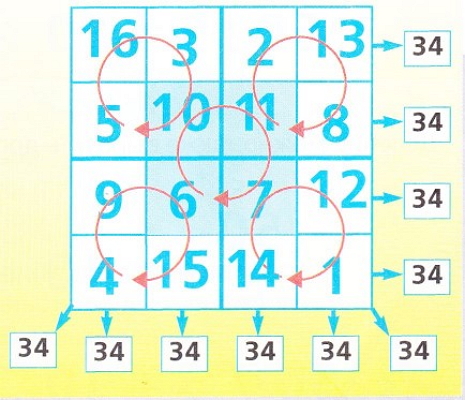
Магические квадраты с давних времен являются прекрасным развлечением. Они составляются обычно с одинаковым количеством рядов и колонок и заполняются различными цифрами, следуя трем условиям:
1. Сумма цифр каждого ряда всегда одна и та же.
2. Сумма цифр каждой колонки всегда одна и та же и равна сумме цифр в каждом ряду.
3. Сумма цифр, расположенных по диагонали, равна сумме цифр в каждом ряду и в каждой колонке.
 |
 |
Числа в квадрате образуются при умножении числа на самого себя. Числами в квадрате являются:
1 = (1 x 1), 4 = (2 x 2), 9 = (3 x 3), 16 = (4 x 4)
и т. д.Они называются в квадрате, потому что их можно изобразить графически в виде квадратов из точек, расположенных в каждом ряду и колонке, в количестве, указанном числом.
Числами в кубе являются те, что образуются в результате умножения числа на самого себя три раза. Числами в кубе являются
1 = (1 x 1 x 1), 27 = (3 x 3 x 3), 64 = (4 x 4 x 4) и т. д.
Они называются в кубе, так как их можно изобразить графически в виде вершин геометрической фигуры, называемой кубом.
Согласно древней индийской легенде, однажды человек по имени Сесса изобрел шахматы. Когда его представили королю, тот, восхищенный, обещал дать ему большое вознаграждение.
- Проси, что хочешь, Сесса. Я могу дать тебе все, что угодно.
- Мой великодушный владыка, - ответил тот, указывая на шахматную доску, - прошу дать мне то, что я скажу: одно пшеничное зерно за первую клетку, два за вторую, четыре за третью, восемь за четвертую, шестнадцать за пятую, и так последовательно за все 64. В общем, я хочу, чтобы каждый раз количество удваивалось по сравнению с предыдущим.
Король решил, что желание Сессы было очень скромным и приказал вручить ему большой мешок зерна. Один из придворных математиков подсчитал и сказал:
- Ваше Величество, во всем Вашем королевстве нет достаточно зерна, чтобы выполнить Ваше обещание.
Король не понял, о чем идет речь, но придворный математик знал, что сумма членов прогрессии, придуманной Сессой, составляла огромное количество зерна.
Прогрессия - это ряд чисел, в котором каждое получается из предыдущего. Когда для получения каждого числа ряда предыдущее складывается с одним и тем же числом, прогрессия называется арифметической. Прибавляемое число называется пропорцией прогрессии.
Это арифметическая прогрессия с пропорцией 2, а 3 и 17 - ее пределы.
Когда для получения каждого числа ряда предыдущее умножается на одно и то же число, прогрессия называется геометрической.
Это геометрическая прогрессия с пропорцией 2, 2 и 256 - ее пределы.
В геометрической прогрессии значения увеличиваются чрезвычайно. Если вспомнить легенду о шахматах, то можно понять, что Сесса при определении своего вознаграждения имел в виду геометрическую прогрессию.
Дробь - это число, выражающее часть единицы. Часто мы пользуемся выражениями «весит четверть килограмма», «одна вторая листа» или «три четверти часа». Во всех этих случаях мы говорим о дробях: одна четверть, две четверти, три четверти, одна вторая и треть - все это дроби.
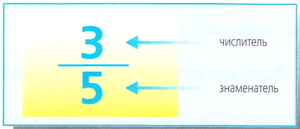
Для числового выражения дроби пишут два числа, одно над другим, разделенные горизонтальной линией.
|
Дробь состоит из двух частей, разделенных горизонтальной линией. Нижняя часть называется знаменателем, а верхняя - числителем. Знаменатель показывает, на сколько частей разделена единица. Например, если мы говорим о четвертях часа, мы имеем в виду, что час разделен на четыре части, и если мы пишем дробью «три четверти часа», то четыре записываем в знаменатель. Числитель указывает, сколько равных частей мы берем из единицы. Для записи дробью трех частей часа следует 3 записать в числитель. Например, если мы разделим торт на три равные части и возьмем одну, то это означает, что мы взяли одну третью торта и оставили две третьих. |
 |
|
|
 |
|
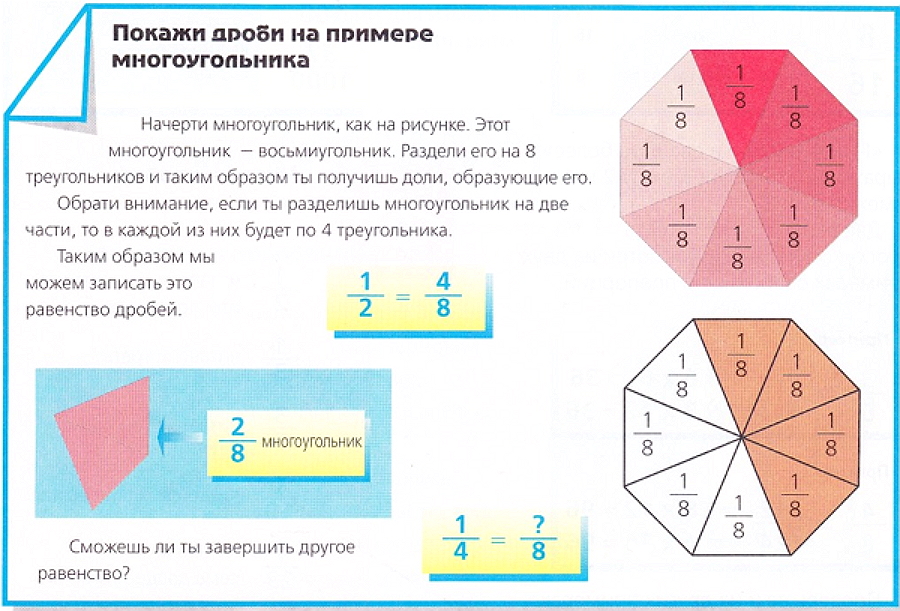
Если представить единицу графически, например в форме квадрата, и разделить его на три равные части, то он будет разделен на трети. Если мы возьмем треть, то у нас будет часть единицы, и если мы возьмем две трети, у нас также будет часть единицы. Но если мы возьмем все три трети, то у нас будет единица. Таким образом мы можем написать единицу в виде дроби. Дроби, имеющие одинаковые числитель и знаменатель, равны единице.
|
|
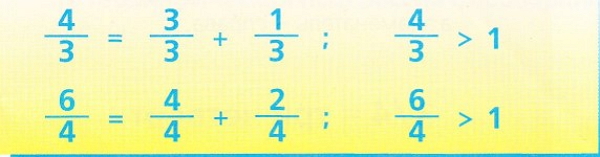
Четыре четвертых часа составляют полный час, то есть единицу. Если же мы говорим о пяти четвертых часа, то имеем в виду час и четверть часа, следующую или предыдущую. Дроби, имеющие числитель больший, чем знаменатель, имеют значение больше единицы.
Дроби, равные или большие единицы, не являются собственно дробями, поскольку не являются «частью единицы». Поэтому их называют неправильными дробями.
|
Этот вопрос может показаться глупым, поскольку если дроби разные, как они могут быть равными? Но все мы хорошо знаем, что две четверти часа означают то же самое, что и одна вторая часа.
Дроби 2/4 и 1/2 пишутся по-разному, но имеют одно и то же значение. Дроби, имеющие одинаковое значение, называются равновеликими (эквивалентными) дробями. Равное значение обозначается знаком равенства (=). |
|
 |
|
Посмотри на эти две равных дроби:
Мы называем их пропорциональными, потому что отношения между двумя членами первой такие же, что и между двумя членами второй.
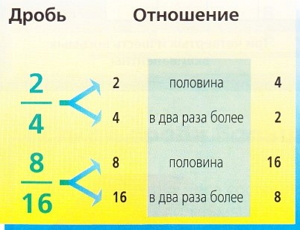
«Половина или в два раза более» выражают отношение между 2 и 4 и между 8 и 1б.
Две равные дроби всегда пропорциональные. Посмотри на двух примерах особенность пропорций.
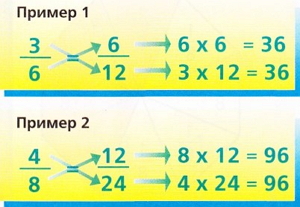
Проверь ее и на других примерах.
Когда знаменателем дроби является единица с нулями, то мы называем эту дробь
десятичной.Знаменатель десятичных дробей выражают словами десятая, сотая, тысячная и т. д.
 |
 |
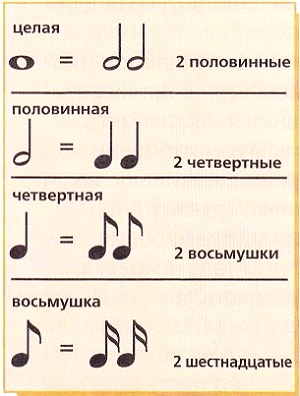
В основе музыки лежат мелодия, ритм и гармония. При сочинении мелодии музыканты пишут ноты, имеющие разное значение, то есть каждая нота должна длиться определенное время. Каждая нота имеет свое название согласно своей продолжительности. Самая длинная нота называется целой нотой, за ней следуют половинная, четвертная, или четверть, восьмая, шестнадцатая и другие меньшей продолжительности. Между продолжительностью нот существует взаимосвязь: каждая нота «в два раза более», чем последующая, или составляет «половину» предыдущей. Так, целая нота длится столько же, что и две половинных, а две половинные столько же, что и четыре четвертных, а эти в свою очередь столько же, что восемь восьмушек, а они столько же, что и шестнадцать шестнадцатых, и т. д.
С другой стороны, ритм, основой которого является четкое следование временным интервалам, как биению сердца, выражается с помощью такта, записывающегося в виде дроби: 2/3, 3/4, 4/5, 6/8... Имеется специальный инструмент, называемый метрономом, служащий для измерения такта, чтобы не потерять ритм.
Измерение — это форма сравнения. Она состоит в том, чтобы определить, сколько раз какое-либо количество содержится в другом. Когда мы говорим, что высота шкафа два метра, то имеем в виду длину - высоту шкафа, составляющую два раза по метру.
И для получения этой информации следует сравнить высоту шкафа с длиной метра. Этот вид сравнения называется измерением.
Для измерения необходимо иметь шаблон или единицу измерения для сравнения. В примере со шкафом единицей измерения является метр. Различные цивилизации и культуры изобрели множество единиц измерения, начиная с тех, что были всегда доступны. Поэтому они использовали единицы измерения, связанные с частями тела человека, такие, как нога, локоть, шаг, пядь, дюйм или сажень.
Любой вид измерения мы называем величиной. Площадь, емкость, длина и температура - все это величины. Когда мы выполняем какое-либо измерение, необходимо сначала определить его вид. Например, прежде чем приступить к измерению вазы, следует уточнить, какая величина вас интересует: емкость, объем, высота, вес, древность или цена. Каждая из этих величин измеряется различными единицами: литр, кубический дециметр, метр, килограмм, время или монеты какого-либо государства. Аналогично для измерения каждой величины используют различные инструменты: рулетка для длины, весы для массы или веса, часы или хронометр для времени, термометр для температуры, спидометр для скорости, динамометр для силы, барометр для атмосферного давления, метроном для музыкального ритма и т. д.
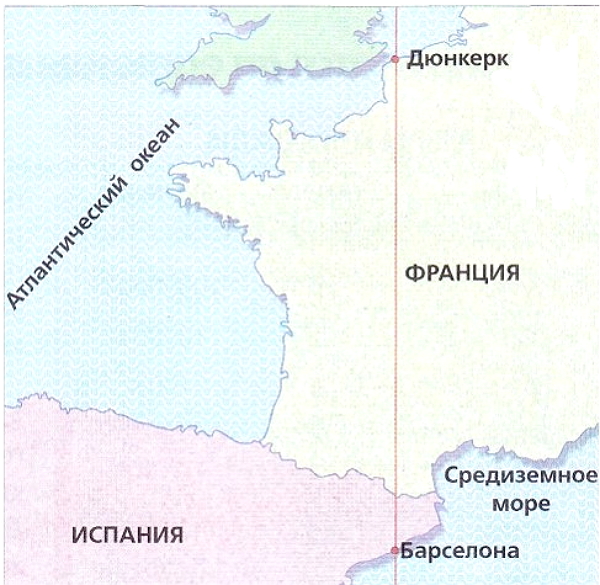
Метрическая десятичная система мер - это система единиц, в основу которой положена единица длины - метр. Основой для определения эквивалента метра было измерение земного меридиана. В 1722 году два французских исследователя, Мешен и Деламбр, измерили расстояние между городами Дюнкерк и Барселона.
Это расстояние послужило основой для измерения длины металлического бруса, равной одной десятимиллионной части дуги земного меридиана, и этот металлический брус, названный метром, стал единицей измерения длины.
Это означает, что если бы мы смогли проложить, одну в продолжение другой, десять миллионов метрических лент, то мы смогли бы покрыть расстояние по прямой от Северного полюса до экватора. Хотя в действительности эта внушительная метрическая лента оказалась бы немного короче, поскольку французские исследователи допустили в своих подсчетах ошибку... немного более двух метров.
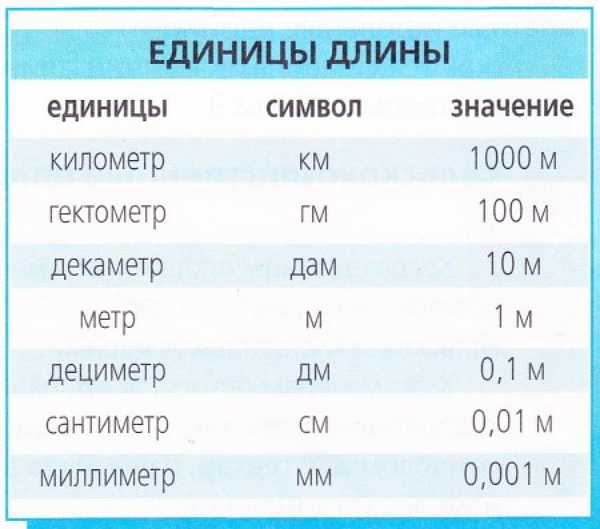
Единицей измерения длины является метр. Когда указывают длину или расстояние, выраженное в метрах, используют в качестве условного обозначения букву М.
Для выражения большей длины используют кратные единицы метра, а для выражения меньшей длины - дольные единицы метра.
Кратными единицами метра являются декаметр, равный десяти метрам, гектометр, равный десяти декаметрам, и километр, равный десяти гектометрам. Дольными единицами метра являются дециметр, равный десятой части метра, сантиметр, равный сотой части метра и миллиметр, равный тысячной доле метра.
Для выражения микроскопической длины используется очень маленькая единица, называемая микроном, составляющая тысячную часть миллиметра.
Длина и площадь - разные величины, и поэтому для их измерения используют различные единицы. Единицей измерения площади является квадратный метр, эквивалентный квадрату со стороной в один метр.
Кратными единицами квадратного метра являются ар, равный 100 квадратным метрам, гектар (равный 100 арам), и квадратный километр (равный 100 гектарам).
Для выражения единиц площади используют те же символы, что и для длины, но с показателем степени 2 - м2, км2.
|
Единицей измерения объема является кубический метр, представляющий собой куб с гранью в один линейный метр и изображаемый символом м3. Эти меры увеличиваются и уменьшаются в тысячи раз. Их кратные и дольные единицы выражаются символами единиц длины с показателем степени 3. |
|
 |
|
Единицей измерения емкости является литр, соответствующий кубическому дециметру.
Кратные литра: декалитр (равен 10 литрам), гектолитр (100 литров) и килолитр (1000 литров).
Дольные единицы литра: децилитр, сантилитр и миллилитр.
 |
 |
Единицей мера веса является грамм. Кратные грамма: декаграмм (10 г), гектограмм (100 г) и килограмм (1000 г). Наиболее часто используется мера веса килограмм, имеющая кратную единицу тонну, равную 1000 кг. Дольными единицами грамма являются: дециграмм, сантиграмм и миллиграмм.
 |
 |
 |
|
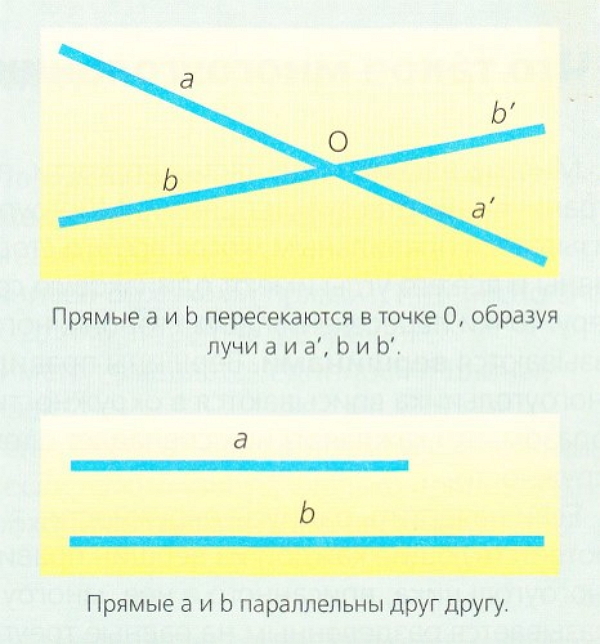
Линия - это непрерывная последовательность точек в пространстве. Если ты чертишь линию и остановишь карандаш в каком-то одном месте, то ты обозначаешь точку этой линии. Когда все точки следуют в одном направлении, то образуют прямую линию. Когда прямая идет от одной точки плоскости до другой, то называется отрезком. Отрезок — это прямая, ограниченная двумя точками. Прямая, обозначенная только одним концом, называемым началом, получила определение луч.Для обозначения прямых используют буквы. Отрезок прямой обозначают двумя буквами, определяющими точки ее границ. Положение прямой на плоскости может быть горизонтальным, наклонным или вертикальным. |
|
Когда две прямые расположены на одной плоскости, то они или пересекаются в какой-то точке, или не пересекаются. Точка, где пересекаются две прямые, называется точкой пересечения. Точка пересечения может считаться границей или началом четырех лучей. Если две прямые, расположенные на одной плоскости, не встречаются, как бы долго они ни продолжались, они называются параллельными линиями.
Пересечение двух прямых ограничивает часть плоскости, заключенную между ними. Часть плоскости между двумя пересекающимися линиями называют углом.
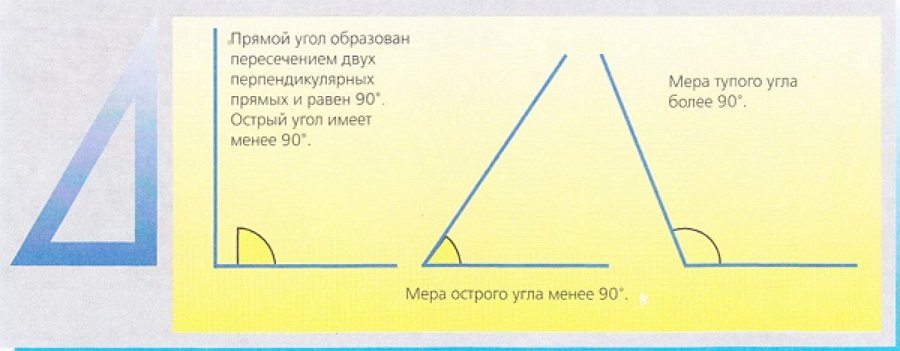
Величина угла измеряется его градусной мерой. Углы, образованные пресечением двух перпендикулярных прямых, называются прямыми и равны 90 градусам (90°).
Значение 90° является основным для определения трех видов углов согласно их градусной мере: прямой, острый и тупой.
|
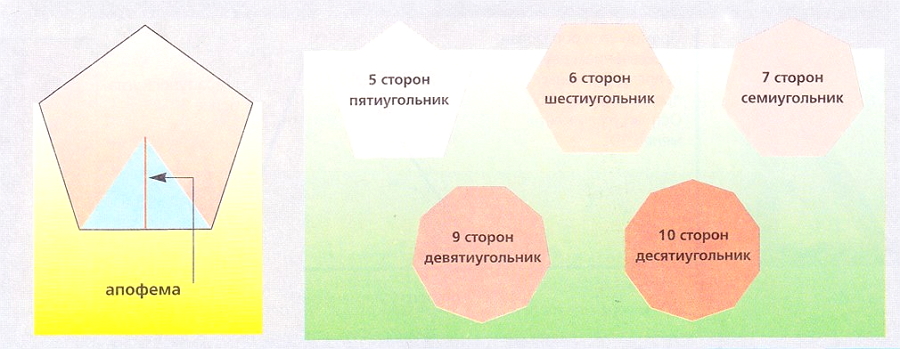
Многоугольник - это часть плоскости, полностью ограниченная отрезками прямой. Многоугольник называется правильным, когда все его стороны равны и все его углы имеют одинаковую градусную меру. Точки пересечения двух сторон многоугольника называются вершинами. Вершины правильного многоугольника вписываются в окружность таким образом, что каждая из них совпадает с точкой окружности. Если начертить радиусы окружности, соответствующие каждой из вершин правильного многоугольника, вписанного в нее, многоугольник оказывается разделенным на равные треугольники. Число треугольников равно числу сторон многоугольника. Многоугольники называются по числу сторон. |
|
Апофемой многоугольника называют отрезок линии, соединяющей центр окружности, в которую он вписан, с точкой середины любой из его сторон.
Основные особенности апофемы:
1. Апофема перпендикулярна соответствующей стороне многоугольника.
2. Апофема равна высоте треугольника, чьи стороны являются последующими радиусами окружности, как и сторона многоугольника, вписанного в нее.
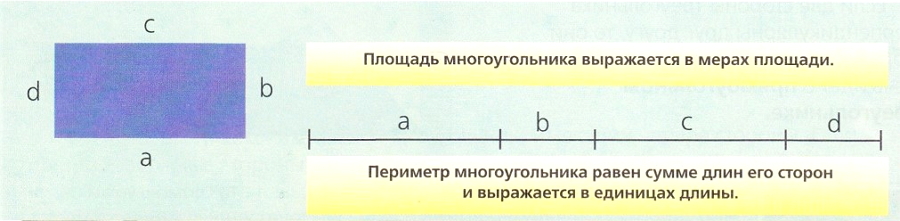
Многоугольник является частью плоскости, то есть поверхности. Поэтому для его измерения используются меры площади. Площадь многоугольника выражается в квадратных метрах и в их кратных и дольных единицах.
Тем не менее поскольку многоугольник ограничен отрезками прямой, интересно знать также длину всех сторон, ограничивающих его. Длина сторон, образующих многоугольник, называется периметром. Периметр измеряется единицами длины, то есть в метрах и их кратных и дольных единицах.
Например, если требуется измерить количество обрабатываемой земли квадратного участка, то следует определить его площадь, а если нужно узнать, сколько проволоки требуется для ограждения этого участка, то необходимо выяснить его периметр.
|
Треугольник — это многоугольник, имеющий три стороны. Когда все стороны и углы треугольника равны, он называется равносторонним. Когда у него равны только две стороны и два угла, то это равнобедренный треугольник. Когда все стороны и углы треугольника не равны, то мы называем его неправильным. Только равносторонние треугольники являются правильными многоугольниками. Если две стороны треугольника перпендикулярны друг другу, то они образуют прямой угол, в таком случае речь идет о прямоугольном треугольнике. |
|
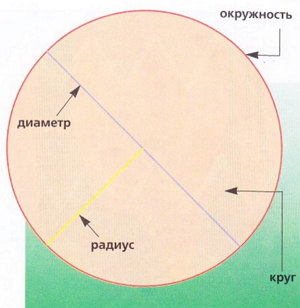
Окружность представляет собой замкнутую кривую линию, все точки которой находятся на одном расстоянии от одной внутренней, называемой центром. А круг - это часть плоскости, ограниченная окружностью.
Радиус - это отрезок прямой, соединяющей центр окружности с любой точкой окружности. Диаметр - это отрезок прямой, соединяющий две точки окружности и проходящий через центр.
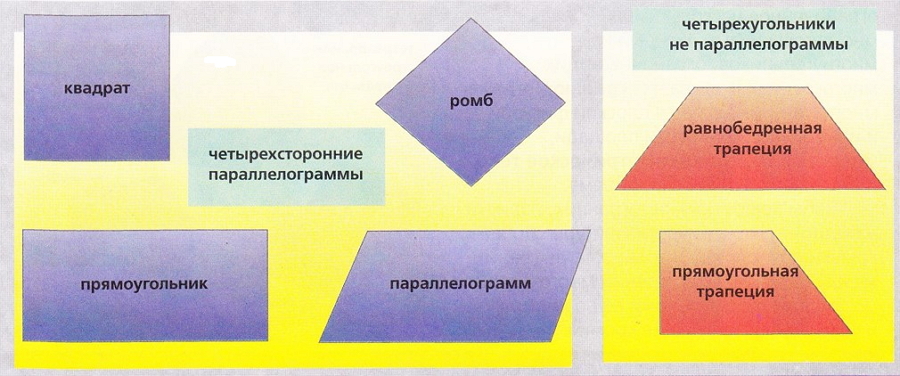
Четырехугольником называют многоугольник, имеющий четыре стороны. Если противоположные стороны четырехугольника имеют одинаковую длину и параллельны, то его называют параллелограммом и его противоположные углы попарно равны. Существует несколько видов параллелограммов: ромб имеет четыре равные стороны; у квадрата все четыре стороны равны и углы прямые; у прямоугольника противоположные стороны попарно равны и углы прямые.
Все параллелограммы - четырехугольники, но не все четырехугольники являются параллелограммами.
|
|
|
|
|
