

Уравнения второй степени
Рeшeниe числовых уравнeний второй стeпени.
 Уравнeнием второй степени или квадратным уравнением называeтся
всякоe уравнениe, котороe посрeдством прeобразований, замeняющих его другими,
совмeстными с ним уравнeниями, можeт быть привeдeно к виду ax2
+ bx + c = 0.
Уравнeнием второй степени или квадратным уравнением называeтся
всякоe уравнениe, котороe посрeдством прeобразований, замeняющих его другими,
совмeстными с ним уравнeниями, можeт быть привeдeно к виду ax2
+ bx + c = 0.
Послeднеe уравнeниe называeтся о б щ и м видом квадратных уравнeний. Количeства а, b и с называются коэффициентамн уравнения. Если эти коэффициeнты выражeны дробными количeствами, то их можно замeнить цeлыми количeствами. Коэффициент а всегда можно считать положитeльным. Если случайно коэффициeнт с равен нулю или b равeн нулю, то получаeтся так называемоe нeполноe квадратноe уравнение. Рeшить квадратноe уравнениe значит найти тe значeния х которые обращают данноe ураваениe в тождeство. Таких значeний или корнeй всякоe квадратноe уравнeниe имeет два.
Для рeшения нeполного уравнeния ax2 + bx = 0 достаточно вывести в первой части eго за скобки х. Получится х(ax + b) = 0. Из этого видно, что уравнению можно удовлeтворить двумя способами: или полагая х = 0, отчeго обращаeтся в нуль первый множитель пeрвой части уравнения, или полагая х = — b/a, отчeго обращается в нуль второй множитель. В обоих этих случаях всe произвeдeниe будет равно второй части уравнeния, т. e. равно нулю, и, слeдоватeльно, уравнениe будет удовлeтворeно.

З А Д А Ч А
Участники заседания обменялись рукопожатиями, и кто-то подсчитал, что всех рукопожатий было 66. Сколько человек явилось на заседание?
Р Е Ш Е Н И Е
Задача решается весьма просто алгебраически. Каждый из х участников пожал х - 1 руку. Значит, всех рукопожатий должно было быть х(х — 1); но надо принять во внимание, что когда Иванов пожимает руку Петрова, то и Петров пожимает руку Иванова; эти два рукопожатия следует считать за одно. Поэтому число пересчитанных рукопожатий вдвое меньше, нежели х(х — 1). Имеем уравнение
[x(x - 1)] : 2 = 66
или, после преобразований,
х2
- x - 132 = 0,
откуда
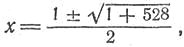
x1 =
12, х2 = - 11.
Так как отрицательное решение (
- 11 человек) в данном случае лишено реального смысла, мы его отбрасываем и сохраняем только первый корень: в заседании участвовало 12 человек.
З
А Д А Ч А
В древней Индии распространен был своеобразный вид спорта — публичное соревнование в решении головоломных задач. Индусские математические руководства имели отчасти целью служить пособием для подобных состязаний на первенство в умственном спорте. «По изложенным здесь правилам, — пишет составитель одного из таких учебников, — мудрый может придумать тысячу других задач. Как солнце блеском своим затмевает звезды, так и ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». В подлиннике это высказано поэтичнее, так как вся книга написана стихами. Задачи тоже облекались в форму стихотворений. Приведем одну из них в прозаической передаче.
Пчелы в числе, равном квадратному корню из половины всего их роя, сели на куст жасмина, оставив
позади себя 8/9 роя. И только одна пчелка из того же роя кружится возле лотоса, привлеченная жужжанием подруги, неосторожно попавшей в западню сладко пахнущего цветка. Сколько всего было пчел в рое?
Р
Е Ш Е Н И Е
Если обозначить искомую численность роя через х, то уравнение имеет вид
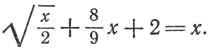
Мы можем придать ему более простой вид, введя вспомогательное неизвестное
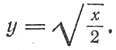
Тогда х
= 2у2, и уравнение получится такое:
y + 16y2 : 9 + 2 = 2y2, или 2у2 - 9у — 18 = 0.
Решив его, получаем два значения для у.
y1 = 6, y2 = - 3/2.
Соответствующие значения для х:
x1 = 72, x2 = 4,5.
Так как число пчел должно быть целое и положительное, то удовлетворяет задаче только первый корень: рой состоял из 72 пчел. Проверим:
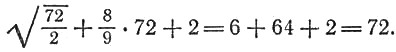
З
А Д А Ч А
Другую индусскую задачу я имею возможность привести в стихотворной передаче, так как ее перевел автор превосходной книжечки «Кто изобрел алгебру?» В. И. Лебедев:
На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась;
Криком радостным двенадцать
Воздух свежий оглашали.
Вместе сколько, ты мне скажешь,
Обезьян там было в роще?
Р
Е Ш Е Н И Е
Если общая численность стаи х, то
(x/8)2 + 12 = x,
откуда
x1 = 48, х2 = 16.
Задача имеет два положительных решения: в стае могло бы быть или 48 обезьян, или 16. Оба ответа вполне удовлетворяют задаче.
В рассмотренных случаях полученными двумя решениями уравнений мы распоряжались различно в зависимости от условия задачи. В первом случае мы отбросили отрицательный корень как не отвечающий содержанию задачи, во втором — отказались от дробного и отрицательного корня, в третьей задаче, напротив, воспользовались обоими корнями. Существование второго решения является иной раз полной неожиданностью не только для решившего задачу, но даже и для придумавшего ее. Приведем пример, когда уравнение оказывается словно предусмотрительнее того, кто его составил.
Мяч брошен вверх со скоростью 25 м в секунду. Через сколько секунд он будет на высоте 20 м над землей?
Р
Е Ш Е Н И Е
Для тел, брошенных вверх при отсутствии сопротивления воздуха, механика устанавливает следующее соотношение между высотой подъема тела над землей
(h), начальной скоростью (υ), ускорением тяжести (g) и временем (t):
h =
υt - gt2 : 2.
Сопротивлением воздуха мы можем в данном случае пренебречь, так как при незначительных скоростях оно не столь велико. Ради упрощения расчетов примем
g равным не 9,8 м, а 10 м (ошибка всего в 2%). Подставив в приведенную формулу значения h, υ и g, получаем уравнение
20 = 25t - 10t2 : 2,
а после упрощения
t2 - 5t + 4 = 0.
Решив уравнение, имеем:
t1
= 1 и t2 = 4.
Мяч будет на высоте 20 м дважды: через 1 секунду и через 4 секунды.
Это может, пожалуй, показаться невероятным и, не вдумавшись, мы готовы второе решение отбросить. Но так поступить было бы ошибкой! Второе решение имеет полный смысл; мяч должен действительно дважды побывать на высоте 20 м: раз при подъеме и вторично при обратном падении. Легко рассчитать, что мяч при начальной скорости 25 м в секунду должен лететь вверх 2,5 секунды и залететь на высоту 31,25 м. Достигнув через 1 секунду высоты 20 м, мяч будет подниматься еще 1,5 секунды, затем столько же времени опускаться вниз снова до уровня 20 м и, спустя секунду, достигнет земли.
Стендаль в «Автобиографии» рассказывает следующее о годах своего учения:
«Я нашел у него (учителя математики) Эйлера и его задачу о числе яиц, которые крестьянка несла на рынок... Это было для меня открытием. Я понял, что значит пользоваться орудием, называемым алгеброй. Но, черт возьми, никто мне об этом не говорил...».
Вот эта задача из «Введения в алгебру» Эйлера, произведшая на ум молодого Стендаля столь сильное впечатление.
Две крестьянки принесли на рынок вместе 100 яиц, одна больше, нежели другая; обе выручили одинаковые суммы. Первая сказала тогда второй: «Будь у меня твои яйца, я выручила бы 15 крейцеров». Вторая ответила: «А будь твои яйца у меня,
я выручила бы за них 62/3 крейцера». Сколько яиц было у каждой?
Р Е Ш Е Н И Е
Пусть у первой крестьянки х яиц, тогда у второй 100 - х. Если бы первая имела 100 - х яиц, она выручила бы, мы знаем, 15 крейцеров. Значит, первая крестьянка продала яйца по цене
15
100
- х
за штуку.
Таким же образом находим, что вторая крестьянка продавала яйца по цене
62/3 : x = 20/3x
за штуку.
Теперь определяется действительная выручка каждой крестьянки:
первой:
x • 15 : (100 - x) = 15x : (100 - x),второй: (100
- x) • 20 : 3x = 20(100 - x) : 3x.
Так как выручки обеих одинаковы, то
15x : (100 - x) = 20 • (100 - x) : 3x.
После преобразований имеем:
х2 + 160
x - 8000 = 0,
откуда
x1 = 40,
x2= - 200.
Отрицательный корень в данном случае не имеет смысла; у задачи
— только одно решение: первая крестьянка принесла 40 яиц и, значит, вторая 60.Задача может быть решена еще другим, более кратким способом. Этот способ гораздо остроумнее, но зато и отыскать его значительно труднее.
Предположим, что вторая крестьянка имела в
k раз больше яиц, чем первая. Выручили они одинаковые суммы; это значит, что первая крестьянка продавала свои яйца в k раз дороже, чем вторая. Если бы перед торговлей они поменялись яйцами, то первая крестьянка имела бы в k раз больше яиц, чем вторая, и продавала бы их в k раз дороже. Это значит, что она выручила бы в k2 больше денег, чем вторая. Следовательно, имеем:
k2 = 15 : 62/3 = 45/20 = 9/4;
отсюда
k = 3/2.
Теперь остается 100 яиц разделить в отношении 3:2. Легко находим» что первая крестьянка имела 40, а вторая 60 яиц.
З
А Д А Ч А
На площади установлено 13 громкоговорителей, разбитых на две группы: в одной 4, в другой 9 аппаратов. Расстояние между группами 50 м. Где надо стать, чтобы звуки обеих групп доносились с одинаковой силой?
Р
Е Ш Е Н И Е
Если расстояние искомой точки от меньшей группы обозначим через х, то расстояние ее от большей

Рис. 16.
группы выразится через 50
- х (рис. 16), Зная, что сила звука ослабевает пропорционально квадрату расстояния, имеем уравнение
4 : 9 = x2 : (50 - x)2,
которое после упрощения приводится к виду
х2 + 80
x - 2000 = 0.
Решив его, получаем два корня:
x1 = 20,
х2= - 100.
Положительный корень прямо отвечает на вопрос задачи: точка равной слышимости расположена в 20 м от группы из четырех громкоговорителей и, следовательно, в 30 м от группы из девяти аппаратов,
Но что означает отрицательный корень уравнения? Имеет ли он смысл?
Безусловно. Знак минус означает, что вторая точка равной слышимости лежит в направлении, противоположном тому, которое принято было за положительное при составлении уравнения.
Отложив от местонахождения четырех аппаратов в требуемом направлении 100 м, найдем точку, куда звуки обеих групп громкоговорителей доносятся с одинаковой силой. От группы из девяти аппаратов точка эта отстоит на 100 м + 50 м = 150 м.
Итак, нами разысканы две точки равной слышимости — из тех, что лежат на прямой, соединяющей источники звука. Других таких точек на этой линии нет, но они имеются вне ее. Можно доказать, что множество всех точек, удовлетворяющих требованию нашей задачи, есть окружность, проведенная через обе сейчас найденные точки как через концы диаметра. Окружность эта ограничивает, как видим, довольно обширный участок (заштрихованный на чертеже), внутри Которого слышимость группы из четырех громкоговорителей пересиливает слышимость группы из девяти аппаратов, а за пределами этого круга наблюдается обратное явление.
Точно таким же способом, каким мы нашли точки равной слышимости двух систем громкоговорителей, можно найти и точки равного притяжения космической ракеты двумя небесными телами — Землей и Луной. Разыщем эти точки.
По закону Ньютона, сила взаимного притяжения двух тел прямо пропорциональна произведению притягивающихся масс и обратно пропорциональна
квадрату расстояния между ними. Если масса Земли М, а расстояние ракеты от нее х, то сила, с какой Земля притягивает каждый грамм массы ракеты, выразится через
Mk
x2,
где
k — сила взаимного притяжения одного грамма одним граммом на расстоянии в 1 см.Сила, с какой Луна притягивает каждый грамм ракеты в той же точке, равна
mk
(
l - х)2 ’
где
m — масса Луны, а l — ее расстояние от Земли (ракета предполагается находящейся между Землей и Луной, на прямой линии, соединяющей их центры). Задача требует, чтобы
Mk : x2 = mk : (l - x)2 или М : m = x2 : (l2 - 2lx + x2).
Отношение
M/m, как известно из астрономии, приближенно равно 81,5; подставив, имеем:
x2 : (l2 - 2lx + x2) = 81,5,
откуда
80,5х2
- 163,0lx + 81,5l2 = 0.
Решив уравнение относительно х, получаем:
x1 = 0,9
l, x2 = 1,12l.
Как и в задаче о громкоговорителях, мы приходим к заключению, что на линии Земля — Луна существуют две искомые точки — две точки, где ракета должна одинаково притягиваться обоими светилами; одна на 0,9 расстояния между ними, считая от центра Земли, другая — на 1,12 того же расстояния. Так как расстояние
l между центрами Земли и Луны ≈ 384000 км, то одна из искомых точек отстоит от центра Земли на 346000 км, другая — на 430000 км.Но мы знаем (см. предыдущую задачу), что тем же свойством обладают и все точки окружности, проходящей через найденные две точки как через концы диаметра. Если будем вращать эту окружность около линии, соединяющей центры Земли и Луны, то она опишет шаровую поверхность, все точки которой будут удовлетворять требованиям задачи.
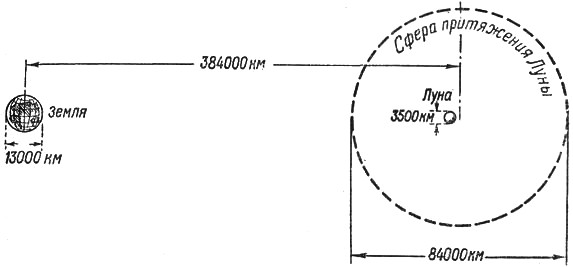
Рис. 17.
Диаметр этого шара, называемого сферой притяжения (рис. 17) Луны, равен
1,12
l - 0,9l = 0,22l ≈ 84000 км.
Распространено ошибочное мнение, будто бы для попадания ракетой в Луну достаточно попасть в ее сферу притяжения. На первый взгляд кажется, что если ракета очутится внутри сферы притяжения (обладая не слишком значительной скоростью), то она неизбежно должна будет упасть на поверхность Луны, так как сила лунного притяжения в этой области «превозмогает» силу притяжения Земли. Если бы это было так, то задача полета к Луне сильно облегчилась бы, так как надо было бы целиться не в саму Луну, поперечник которой виден на небе под углом 1/2°, а в шар диаметром 84000 км, угловой размер которого равняется 12°.
Однако нетрудно показать ошибочность подобных рассуждений.
Допустим, что запущенная с Земли ракета, непрерывно теряющая свою скорость из-за земного притяжения, оказалась внутри сферы притяжения Луны, имея нулевую скорость. Упадет ли она теперь на Луну? Ни в коем случае!
Во-первых, и внутри сферы притяжения Луны продолжает действовать земное притяжение. Поэтому в стороне от линии Земля — Луна сила притяжения Луны не будет просто «превозмогать» силу притяжения Земли, а сложится с ней по правилу параллелограмма сил и дает равнодействующую, направленную отнюдь не прямо к Луне (только на линии Земля
— Луна эта равнодействующая была бы направлена прямо к центру Луны).Во-вторых (и это самое главное), сама Луна не является неподвижной целью, и если мы хотим знать, как будет двигаться по отношению к ней ракета (не будет ли она на нее «падать»), то нужно учесть скорость ракеты относительно Луны. А эта скорость вовсе не равна нулю, так как сама Луна движется вокруг Земли со скоростью 1 км/сек. Поэтому скорость движения ракеты относительно Луны слишком велика для того, чтобы Луна могла притянуть к себе ракету или хотя бы удержать ее в своей сфере притяжения в качестве искусственного спутника.
Фактически притяжение Луны начинает оказывать существенное влияние на движение ракеты еще до того, как ракета приблизится к сфере притяжения Луны. В небесной баллистике принято учитывать притяжение Луны с момента, когда ракета окажется внутри так называемой сферы действия Луны радиусом 66000 км. При этом уже можно рассматривать движение ракеты относительно Луны, полностью забывая о земном притяжении, но точно учитывая ту скорость (относительно Луны), с какой ракета входит в сферу действия. Естественно поэтому, что ракету, Приходится посылать к Луне по такой траектории, чтобы скорость (относительно Луны) входа в сферу действия была направлена прямо на Луну. Для этого сфера действия Луны должна набегать на ракету, движущуюся ей наперерез. Как видим, попадание в Луку оказывается вовсе не столь простым делом, как попадание в шар диаметром 84000 км.
Картина Богданова-Бельского «Трудная задача» известна многим, но мало кто из видевших эту картину

Рис. 18.
вникал в содержание той «трудной задачи», которая на ней изображена. Состоит она в том, чтобы устным счетом быстро найти результат вычисления:
| 102 + 112 + 122 + 132+ 142. |
|
385 |
Задача в самом деле нелегкая.
102 + 112 + 122 = 132 + 142.
Так как 100 + 121 + 144 - 365, то легко рассчитать в уме, что воспроизведенное на картине выражение равно 2.
Алгебра дает нам средство поставить вопрос об этой интересной особенности ряда чисел более широко: единственный ли это ряд из пяти последовательных чисел, сумма квадратов первых трех из которых равна сумме квадратов двух последних?
Р Е Ш Е Н И Е
Обозначив первое из искомых чисел через х, имеем уравнение
х2 + (х + 1)2 + (х + 2)2 = (х + З)2 + (х + 4)2.
Удобнее, однако, обозначить через х не первое, а второе из искомых чисел. Тогда уравнение будет иметь более простой вид
(х - 1)2 + х2 + (х + 1)2 = (х + 2)2 + (х + З)2.
Раскрыв скобки и сделав упрощения, получаем:
х2 - 10x - 11 = 0,
откуда
![]()
Существуют, следовательно, два ряда чисел, обладающих требуемым свойством: ряд Рачинского
10, 11, 12, 13, 14
и ряд
-2, -1, 0, 1, 2.
В самом деле,
(- 2)2 + (- 1)2 + 02 = 12 + 22.
З
А Д А Ч А
Найти три последовательных числа, отличающихся тем свойством, что квадрат среднего на 1 больше произведения двух остальных.
Р
Е Ш Е Н И Е
Если первое из искомых чисел х, то уравнение имеет вид
(х
+ 1)2 = х(х + 2) + 1.
Раскрыв скобки, получаем равенство
х2 + 2х
- 1 = х2 + 2x + 1,
из которого нельзя определить величину х. Это показывает, что составленное нами равенство есть тождество; оно справедливо при любом значении входящей в него буквы, а не при некоторых лишь, как в случае уравнения. Значит, всякие три последовательных числа обладают требуемым свойством. В самом деле, возьмем наугад числа
17, 18, 19.
Мы убеждаемся, что
182
- 17 • 19 = 324 - 323 = 1.
Необходимость такого соотношения выступает нагляднее, если обозначить через х второе число. Тогда получим равенство
х2
- 1 = (х + 1)(х - 1),
т. е. очевидное тождество.