Мой сайт

Прогрессии

Арифметическая прогрессия

Арифмети́ческая прогре́ссия (алгебраическая) — числовая последовательность вида

a₁, a₁ + d, a₁ + 2d, . . . , a₁ + (n - 1)d, . . . ,

то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d (шага, или разности прогрессии):

a_n = a_n_-1 + d

Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:

a_n = a₁ + (n - 1)d

Арифметическая прогрессия является монотонной последовательностью . При d>0 она является возрастающей, а при d<0 — убывающей. Если d = 0, то последовательность будет стационарной. Эти утверждения следуют из соотношения a_n₊₁ - a_n = d для членов арифметической прогрессии.

Геометрическая прогрессия

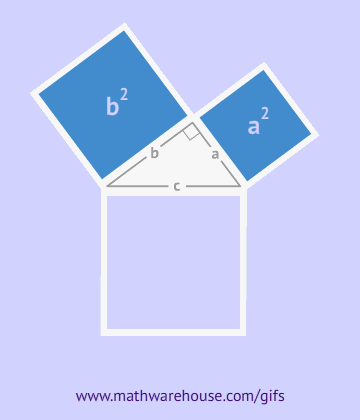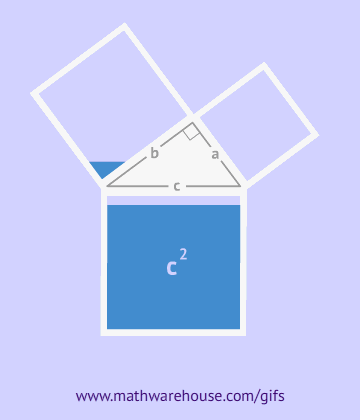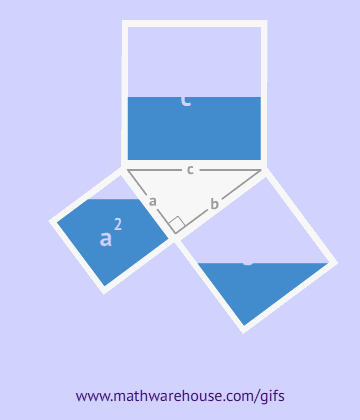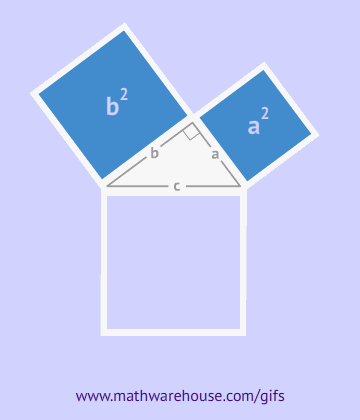
Геометри́ческая прогре́ссия — последовательность чисел b₁, b₂, b₃, . . . (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где

b₁ ≠ 0, q ≠ 0: b₁, b₂ = b₁q, b₃ = b₂q, . . . , b_n = b_n_-1q.

Любой член геометрической прогрессии может быть вычислен по формуле:

b_n = b₁qⁿ^-1

Если b₁ > 0 и q > 1, прогрессия является возрастающей последовательностью, если 0 < q < 1, — убывающей последовательностью, а при q < 0 —знакочередующейся. Своё название прогрессия получила по своему характеристическому свойству:

$|b_{n}| = \sqrt{b_{n-1} b_{n+1}},$

то есть каждый член равен среднему геометрическому его соседей.

Древнейшая прогрессия

З А Д А Ч А

Древнейшая задача на прогрессии — не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом в конце прошлого столетия, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая (приводим ее в вольной передаче):

Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Р Е Ш Е Н И Е

Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член х, разность у. Тогда

доля первого . . . . . . . . . . . . . х

» второго . . . . . . . . . . . . . x + у

» третьего . . . . . . . . . . . . .х + 2у

» четвертого . . . . . . . . . . . х + 3у

» пятого . . . . . . . . . . . . . . .х + 4у.

На основании условий задачи составляем следующие два уравнения:

{	х + (х + у) + (х + 2у) + (х + 3у) + (x + 4у) = 100,
	7 [х + (х + у)] = (х + 2у) + (х + 3у) + (х + 4у).

После упрощений первое уравнение получает вид

х + 2у = 20,

а второе:

11х = 2у.

Решив эту систему, получаем:

x = 1²/₃, y = 9¹/₆.

Значит, хлеб должен быть разделен на следующие части

1²/₃, 10⁵/₆, 20, 29¹/₆, 38¹/₃.

Алгебра на клетчатой бумаге

Несмотря на пятидесятивековую древность этой задачи на прогрессии, в нашем школьном обиходе прогрессии появились сравнительно недавно. В учебнике Магницкого, изданном двести лет назад и служившем целых полвека основным руководством для школьного обучения, прогрессии хотя и имеются, но общих формул, связывающих входящие в них величины между собой, в нем не дано. Сам составитель учебника не без затруднений справлялся поэтому с такими задачами. Между тем формулу суммы членов арифметической прогрессии легко вывести простым и наглядным приемом с помощью клетчатой бумаги. На такой бумаге любая арифметическая прогрессия изображается ступенчатой фигурой. Например, фигура ABDC на рис. 33 изображает прогрессию:

2; 5; 8; 11; 14.

Чтобы определить сумму ее членов, дополним чертеж до прямоугольника ABGE. Получим две равные фигуры ABDC и DGEC. Площадь каждой из них

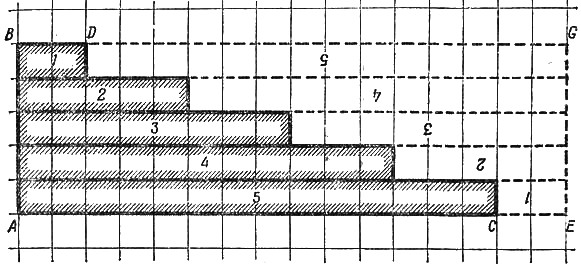
Рис. 33.

изображает сумму членов нашей прогрессии. Значит, двойная сумма прогрессии равна площади прямоугольника ABGE, т. е.

(АС + СЕ) • АВ.

Но АС + СЕ изображает сумму 1-го и 5-го членов прогрессии; АВ — число членов прогрессии. Поэтому двойная сумма

2S = (сумма крайних членов) • (число членов)

или

S =	(первый + последний член) • (число членов)
	2

Поливка огорода

З А Д А Ч А

В огороде 30 грядок, каждая длиной 16 м и шириной 2,5 м. Поливая грядки, огородник приносит ведра с водой из колодца, расположенного в 14 м от края огорода (рис. 34), и обходит грядки по меже, причем воды, приносимой за один раз, достаточно для поливки только одной грядки.

Рис. 34.

Какой длины путь должен пройти огородник, поливая весь огород? Путь начинается и кончается у колодца.

Р Е Ш Е Н И Е

Для поливки первой грядки огородник должен пройти путь

14 + 16 + 2,5 + 16 + 2,5 + 14 = 65 м.

При поливке второй он проходит

14 + 2,5 + 16 + 2,5 + 16 + 2,5 + 2,5 + 14 = 65 + 5 = 70 м.

Каждая следующая грядка требует пути на 5 м длиннее предыдущей. Имеем прогрессию:

65; 70; 75; . . . ; 65 + 5 • 29.

Сумма ее членов равна

(65 + 65 + 29 • 5)30	= 4125 м.
2

Огородник при поливке всего огорода проходит путь в 4,125 км.

Кормление кур

З А Д А Ч А

Для 31 курицы запасено некоторое количество корма из расчета по декалитру в неделю на каждую курицу. При этом предполагалось, что численность кур меняться не будет. Но так как в действительности число кур каждую неделю убывало на 1, то заготовленного корма хватило на двойной срок.

Как велик был запас корма и на сколько времени был он первоначально рассчитан?

Р Е Ш Е Н И Е

Пусть запасено было х декалитров корма на у недель. Так как корм рассчитан на 31 курицу по 1 декалитру на курицу в неделю, то

х = 31y.

В первую неделю израсходовано было 31 дл, во вторую 30, в третью 29 и т. д. до последней недели всего удвоенного срока, когда израсходовано было:

(31 - 2y + 1) дл*).

Весь запас составлял, следовательно,

x = 31y = 31 + 30 + 29 + ... + (31 - 2y + 1).

Сумма 2у членов прогрессии, первый член которой 31, а последний 31 - 2y + 1, равна

31y =	(31 + 31 - 2y + 1)2y	= (63 - 2y)y.
	2

Так как у не может быть равен нулю, то мы вправе обе части равенства сократить на этот множитель. Получаем:

31 = 63 - 2у и y = 16,

откуда

х = 31y = 496.

Запасено было 496 декалитров корма на 16 недель.

_________________________________

*) Поясним: расход корма в течение

1- й недели 31 дл,

2- й » 31 - 1 дл,

3- й » 31 - 2 дл,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2у-й » 31 - (2у - 1) = 31 - 2у + 1 дл.

Бригада землекопов

З А Д А Ч А

Старшеклассники обязались вырыть на школьном участке канаву и организовали для этого бригаду землекопов. Если бы бригада работала в полном составе, канава была бы вырыта в 24 часа. Но в действительности к работе приступил сначала только

Рис. 35.

один член бригады. Спустя некоторое время присоединился второй; еще через столько же времени — третий, за ним через такой же промежуток четвертый и так до последнего. При расчете оказалось, что первый работал в 11 раз дольше последнего.

Сколько времени работал последний?

Р Е Ш Е Н И Е

Пусть последний член бригады работал х часов, тогда первый работал 11х часов. Далее, если число рывших канаву учеников было у, то общее число часов работы определится как сумма у членов убывающей прогрессии, первый член которой 11х, а последний х, т. е.

(11x + x)y	= 6xy.
2

С другой стороны, известно, что бригада из у человек, работая в полном составе, выкопала бы канаву в 24 часа, т. е. что для выполнения работы необходимо 24у рабочих часов.

Следовательно,

6xy = 24у.

Число у не может равняться нулю; на этот множитель можно поэтому уравнение сократить, после чего получаем;

6х = 24

и

х = 4.

Итак, член бригады, приступивший к работе последним, работал 4 часа.

Мы ответили на вопрос задачи; но если бы мы полюбопытствовали узнать, сколько рабочих входило в бригаду, то не могли бы этого определить, несмотря на то, что в уравнении число это фигурировало (под буквой у). Для решения этого вопроса в задаче не приведено достаточных данных.

Яблоки

З А Д А Ч А

Садовник продал первому покупателю половину всех своих яблок и еще пол-яблока, второму покупателю — половину оставшихся и еще пол-яблока; третьему — половину оставшихся и еще пол-яблока и т. д. Седьмому покупателю он продал половину оставшихся яблок и еще пол-яблока; после этого яблок у него не осталось. Сколько яблок было у садовника?

Р Е Ш Е Н И Е

Если первоначальное число яблок х, то первый покупатель получил

x:2 + ¹/₂ = (x + 1):2,

второй

¹/₂х[x - (x + 1):2] +¹/₂ = (x + 1):2²,

третий

¹/₂[x - (x + 1):2 - (x + 1):4] + ¹/₂ = (x + 1):2³,

седьмой покупатель

x + 1

27

Имеем уравнение

(x + 1):2 + (x + 1):2² + (x + 1):2³ + . . . + (x + 1):2⁷ = x

или

(x + 1)(1:2 + 1:2² + 1:2³ + . . . + 1:2⁷) = x.

Вычисляя стоящую в скобках сумму членов геометрической прогрессии, найдем;

x:(x + 1) = 1 - 1:2⁷

и

х = 2⁷ - 1 = 127.

Всех яблок было 127.

Покупка лошади

З А Д А Ч А

В старинной арифметике Магницкого мы находим следующую забавную задачу, которую привожу здесь, не сохраняя языка подлинника:

Некто продал лошадь за 156 руб. Но покупатель, приобретя лошадь, раздумал ее покупать и возвратил продавцу, говоря:

— Нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит.

Тогда продавец предложил другие условия:

— Если по-твоему цена лошади высока, то купи только ее подковные гвозди, лошадь же получишь тогда в придачу бесплатно, Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего ¹/₄ коп., за второй ¹/₂ коп., за третий — 1 коп, и т. д.

Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условия продавца,

Рис. 36.

рассчитывая, что за гвозди придется уплатить не более 10 рублей.

На сколько покупатель проторговался?

Р Е Ш Е Н И Е

За 24 подковных гвоздя пришлось уплатить

¹/₄ + ¹/₂ + 1 + 2 + 2² + 2³ + . . . + 2^24-3

копеек. Сумма эта равна

(2²¹ • 2 - ¹/₄):(2 - 1) = 2²² - ¹/₄ = 4194303³/₄ коп.,

т. е. около 42 тысяч рублей. При таких условиях не обидно дать и лошадь в придачу.

Вознаграждение воина

З А Д А Ч А

Из другого старинного русского учебника математики, носящего пространное заглавие:

«Полный курс чистой математики, сочиненный Артиллерии Штык-Юнкером и Математики партикулярным Учителем Ефимом Войтяховским в пользу и употребление юношества и упражняющихся в Математике» (1795), заимствую следующую задачу:

«Служившему воину дано вознаграждение за первую рану 1 копейка, за другую — 2 копейки, за третью — 4 копейки и т. д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран».

РЕШЕНИЕ

Составляем уравнение

65535 = 1 + 2 + 2² + 2³ + ... + 2^х^-1

или

65535 = (2^x-1 • 2 - 1):(2 - 1) = 2^x - 1.

откуда имеем:

65536 = 2^х и x = 16

— результат, который легко находим путем испытаний.

При столь великодушной системе вознаграждения воин должен получить 16 ран и остаться при этом в живых, чтобы удостоиться награды в 655 руб. 35 коп.