
Наибольшие и наименьшие значения


Помещаемые в этой главе задачи принадлежат к весьма интересному роду задач на разыскание наибольшего или наименьшего значения некоторой величины. Они могут быть решены различными приемами, один из которых мы сейчас покажем.
Русский математик П. Л. Чебышев в своей работе «Черчение географических карт» писал, что особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать средствами своими для достижения по возможности большей выгоды.
З А Д А Ч А
Два железнодорожных пути скрещиваются под прямым углом. К месту скрещения одновременно мчатся по этим путям два поезда: один со станции, находящейся в 40 км от скрещения, другой со станции в 50 км от того же места скрещения. Первый делает в минуту 800 м, второй — 600 м.
Через сколько минут, считая с момента отправления, паровозы были в наименьшем взаимном расстоянии? И как велико это расстояние?.
Р Е Ш Е Н И Е
Начертим схему движения поездов нашей задачи. Пусть прямые АВ и
CD — скрещивающиеся пути (рис. 19), Станция В расположена в 40 км от точки скрещения О, станция D — в 50 км от нее. Предположим, что спустя х минут паровозы будут в кратчайшем взаимном расстоянии друг от друга MN = m.
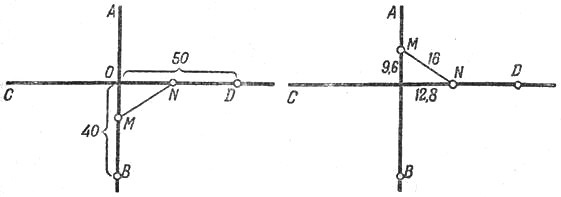
Рис. 19. Рис. 20.
Поезд, вышедший из В, успел к этому моменту пройти путь ВМ = 0,8
x, так как за минуту он проходит 800 м — 0,8 км. Следовательно, ОМ — 40 - 0,8x. Точно так же найдем, что ON = 50 - 0,6x. По теореме Пифагора
![]()
Возвысив в квадрат обе части уравнения
![]()
и сделав упрощения, получаем:
x2 - 124x + 4100 - m2 = 0.
Решив это уравнение относительно х, имеем:
![]()
Так как х — число протекших минут — не может быть мнимым, то m2 - 256 должно быть величиной положительной, или в крайнем случае равняться нулю. Последнее соответствует наименьшему возможному значению m, и тогда
m2 = 256, т. е. m = 16.
Очевидно, что
Итак, паровозы окажутся всего ближе друг к другу через 62 мин., и взаимное их удаление тогда будет 16 км.
Определим, как они в этот момент расположены. Вычислим длину ОМ; она равна
40 - 62 • 0,8 = - 9,6.
Знак минус означает, что паровоз пройдет за скрещение на 9,6 км. Расстояние же ON равно
50 - 62 • 0,6 = 12,8,
т. е. второй паровоз не дойдет до скрещения на 12,8 км. Расположение паровозов показано на рис. 20. Как видим, оно вовсе не то, какое мы представляли себе до решения задачи. Уравнение оказалось достаточно терпимым и, несмотря на неправильную схему, дало правильное решение. Нетрудно понять, откуда эта терпимость: она обусловлена алгебраическими правилами знаков.
З
А Д А Ч А
В стороне от прямолинейного участка железнодорожного пути, в 20 км от него, лежит селение В (рис. 21). Где надо устроить полустанок С, чтобы
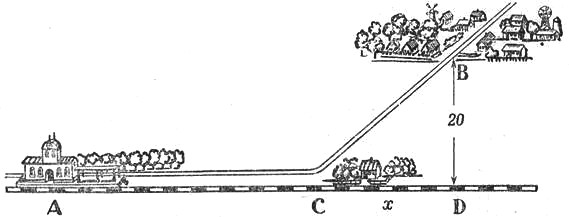
Рис. 21.
проезд от А до В по железной дороге АС и по шоссе СВ отнимал возможно меньше времени? Скорость движения по железной дороге 0,8, а по шоссе 0,2 километра в минуту.
Р
Е Ш Е Н И Е
Обозначим расстояние
AD (от А до основания перпендикуляра BD к AD) через а, CD через х. Тогда АС = AD - СD = а - х, а
![]()
Время прохождения пути СВ по шоссе равно
![]()
Общая продолжительность переезда из А в В равна
![]()
Эта сумма, которую обозначим через m, должна быть наименьшей.
Уравнение
![]()
представляем в виде
![]()
Умножив на 0,8, имеем:
![]()
Обозначив 0,8m - а через k и освободив уравнение от радикала, получаем квадратное уравнение
15х2 - 2kx + 6400 - k2 = 0,
откуда
![]()
Так как k = 0,8m - а, то при наименьшем значении m достигает наименьшей величины и k, и обратно. Но чтобы х было действительным, 16k2 должно быть не меньше 96000. Значит, наименьшая величина для 16k2 есть 96000. Поэтому m становится наименьшим, когда
16k2 = 96000,
откуда
![]()
и следовательно,
![]()
Полустанок должен быть устроен приблизительно в 5 км от точки D, какова бы ни была длина а = AD.
Но, разумеется, наше решение имеет смысл только для случаев, когда х < а, так как, составляя уравнение, мы считали выражение а
- x числом положительным.Если
х = a ≈ 5,16, то полустанка вообще строить не надо; придется вести шоссе прямо на станцию. Так же нужно поступать и в случаях, когда расстояние а короче 5,16 км.На этот раз мы оказываемся предусмотрительнее, нежели уравнение. Если бы мы слепо доверились уравнению, нам пришлось бы в рассматриваемом случае построить полустанок за станцией, что было бы явной нелепостью: в этом случае х > а и потому время
а
- х,0,8
в течение которого нужно ехать по железной дороге, отрицательно. Случай поучительный, показывающий, что при пользовании математическим орудием надо с должной осмотрительностью относиться к получаемым результатам, помня, что они могут потерять реальный смысл, если не выполнены предпосылки, на которых основывалось применение нашего математического орудия.
З А Д А Ч А
Из приречного города А надо направлять грузы в пункт В, расположенный на а километров ниже по реке и в
d километрах от берега (рис. 22). Как
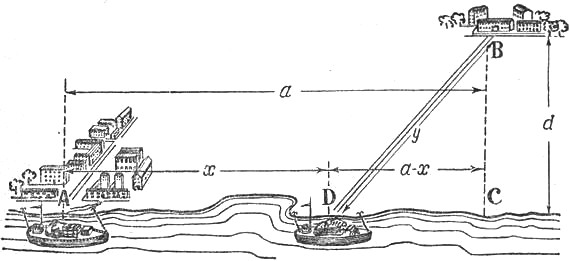
провести шоссе от В к реке, чтобы провоз грузов из А в В обходился возможно дешевле, если провозная плата с тонно-километра по реке вдвое меньше, чем по шоссе?
Р Е Ш Е Н И Е
Обозначим расстояние AD через х и длину DB шоссе — через у: по предположению, длина АС равна а и длина ВС равна d.
Так как провоз по шоссе вдвое дороже, чем по реке, то сумма
х + 2у
должна быть согласно требованию задачи наименьшая. Обозначим это наименьшее значение через
m. Имеем уравнение
х + 2у = m.
Но х
= а -
DC,
a ![]() наше
уравнение получает вид
наше
уравнение получает вид
![]()
или по освобождении от радикала:
Зу2
- 4(m - а)у + (m - а)2 + d2 = 0.
Решаем его:
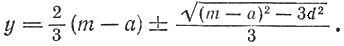
Чтобы у было действительным, (
m - а)2 должно быть не меньше 3d2. Наименьшее значение (m - а)2 равно 3d2, и тогда
![]()
sin < BDC = d : у, т. e.
![]()
Но угол, синус которого равен
![]() равен 60°.
равен 60°.
Значит, шоссе надо провести под углом в 60° к реке, каково бы ни было расстояние АС.
Здесь наталкиваемся снова на ту же особенность, с которой мы встретились в предыдущей задаче. Решение имеет смысл только при определенном условии. Если пункт расположен так, что шоссе, проведенное под углом в 60° к реке, пройдет по ту сторону города А, то решение неприложимо; в таком случае надо непосредственно связать пункт В с городом А шоссе, вовсе не пользуясь рекой для перевозки.
Для решения многих задач «на максимум и минимум», т. е. на разыскание наибольшего и наименьшего значений переменной величины, можно успешно пользоваться одной алгебраической теоремой, с которой мы. сейчас познакомимся. Рассмотрим следующую задачу:
На какие две части надо разбить данное число, чтобы произведение их было наибольшим?
Р Е Ш Е Н И Е
Пусть данное число а. Тогда части, на которые разбито число а, можно обозначить через
a/2 + x и a/2 - x;
число х показывает, на какую величину эти части отличаются от половины числа а. Произведение обеих частей равно
(a:2 + x)(a:2 - x) = a2:4 - x2.
Ясно, что произведение взятых частей будет увеличиваться при уменьшении х, т. е. при уменьшении разности между этими частями. Наибольшим произведение будет при х
= 0, т. е. в случае, когда обе части равны a/2.Итак, число надо разделить пополам: произведение двух чисел, сумма которых неизменна, будет наибольшим тогда, когда эти числа равны между собой.
Рассмотрим тот же вопрос для трех чисел.
На какие три части надо разбить данное число, чтобы произведение их было наибольшим?
Р
Е Ш Е Н И Е
При решении этой задачи будем опираться на предыдущую.
Пусть число а разбито на три части. Предположим
сначала, что ни одна из частей не равна a/2. Тогда среди них найдется часть, большая a/3 (все три не могут быть меньше a/3); обозначим ее через
a/3 + x.
Точно так же среди них найдется часть, меньшая
a/3; обозначим ее через
а/3 - y.
Числа х и у положительны.
Третья часть будет, очевидно, равна
a:3 + y - x.
Числа
a/3 и a/3 + х - у имеют ту же сумму, что и первые две части числа а, а разность между ними, т. е. х - у, меньше, чем разность между первыми двумя частями, которая была равна х + у. Как мы знаем из решения предыдущей задачи, отсюда следует, что произведение
a:3(a:3 + x - y)
больше, чем произведение первых двух частей числа а.
Итак, если первые две части числа а заменить числами
a:3 и a:3 + x - y,
а третью оставить без изменения, то произведение увеличится.
Пусть теперь одна из частей уже равна
a/3. Тогда две другие имеют вид
a/3 + z и a/3 - z.
Если мы эти две последние части сделаем равными
a/3 (отчего сумма их не изменится), то произведение снова увеличится и станет равным
a:3 • a:3 • a:3 = a3:27.
Итак, если число а разбито на 3 части, не равные между собой, то произведение этих частей меньше
чем a3:27, т. е. чем произведение трех равных сомножителей, в сумме составляющих а.Подобным же образом можно доказать эту теорему и для четырех множителей, для пяти и т. д.
Рассмотрим теперь более общий случай.
Найти, при каких значениях х и у выражение
xpyq наибольшее, если х + у = а.
Р Е Ш Е Н И Е
Надо найти, при каком значении х выражение
хр(а - х)q
достигает наибольшей величины.
Умножим это выражение на число
1:ppqq. Получим новое выражение
хр:pp (а — х)q:qq,
которое, очевидно, достигает наибольшей величины тогда же, когда и первоначальное.
Представим полученное сейчас выражение в виде
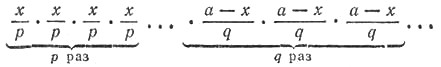
Сумма всех множителей этого выражения равна
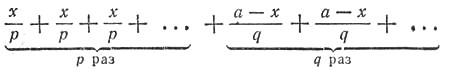
![]()
т. е. величине постоянной.
На основании ранее доказанного заключаем, что произведение
![]()
достигает максимума при равенстве всех его отдельных множителей, т. е. когда
x:p = (a - x):q.
Зная, что а
- х = у, получаем, переставив члены, пропорцию
x:y = p:q.
Итак, произведение
xpyq при постоянстве суммы х + у достигает наибольшей величины тогда, когда
х : у = р : q.
Таким же образом можно доказать, что
произведения
xpyqzr,
при постоянстве сумм х + у + z, х + у + z + t и т. д. достигают наибольшей величины тогда, когда х : у : z = р : q : г, х : у : z : t = р : q : г : u и т. д.
Читатель, желающий испытать свои силы на доказательстве полезных алгебраических теорем, пусть докажет сам следующие положения:
1. Сумма двух чисел, произведение которых неизменно, становится наименьшей, когда эти числа равны.
Например, для произведения 36: 4 + 9=13, 3 + 12 = 15, 2 + 18 = 20, 1 + 36 = 37 и, наконец, 6 + 6= 12.
2. Сумма нескольких чисел, произведение которых неизменно, становится наименьшей, когда эти числа равны.
Например, для произведения 216: 3 + 12 + 6 = 21, 2 + 18 + 6 = 26, 9 + 6 + 4 = 19, между тем как 6 + + 6 + 6=18.
__________________________
На ряде примеров покажем, как применяются на практике эти теоремы.
З А Д А Ч А
Из цилиндрического бревна надо выпилить прямоугольный брус наибольшего объема. Какой формы должно быть его сечение (рис. 23)?

Рис. 23.
Р Е Ш Е Н И Е
Если стороны прямоугольного сечения х и у, то по теореме Пифагора
х2 + у2 =
d2,
где
d — диаметр бревна. Объем бруса наибольший, когда площадь его сечения наибольшая, т. е. когда ху достигает наибольшей величины. Но если ху наибольшее, то наибольшим будет и произведение х2у2. Так как сумма х2 + у2 неизменна, то, по доказанному ранее, произведение х2у2 наибольшее, когда
х2 = у2 или х = у.
Итак, сечение бруса должно быть квадратным.
З А Д А Ч И
1. Какой формы должен быть прямоугольный участок данной площади, чтобы длина ограничивающей его изгороди была наименьшей?
2. Какой формы должен быть прямоугольный участок, чтобы при данной длине изгороди площадь его была наибольшей?
Р Е Ш Е Н И Я
1. Форма прямоугольного участка определяется соотношением его сторон х и у. Площадь участка со сторонами х и у равна ху, а длина изгороди 2
x + 2у. Длина изгороди будет наименьшей, если х + у достигнет наименьшей величины.При постоянном произведении ху сумма х + у наименьшая в случае равенства х
= у. Следовательно, искомый прямоугольник — квадрат.
2. Если х и у — стороны прямоугольника, то длина изгороди 2х + 2у, а площадь ху. Это произведение будет наибольшим тогда же, когда и произведение 4ху, т. е. 2х • 2у; последнее же произведение при постоянной сумме его множителей 2x + 2у становится наибольшим при 2x = 2у, т. е. когда участок имеет форму квадрата.
К известным нам из геометрии свойствам квадрата мы можем, следовательно, прибавить еще следующее: из всех прямоугольников он обладает наименьшим периметром при данной площади и наибольшей площадью при данном периметре.
З А Д А Ч А
Змею, имеющему вид кругового сектора, желают придать такую форму, чтобы он вмещал в данном периметре наибольшую площадь. Какова должна быть форма сектора?
Р Е Ш Е Н И Е
Уточняя требование задачи, мы должны разыскать, при каком соотношении длины дуги сектора и его радиуса площадь его достигает наибольшей величины при данном периметре.
Если радиус сектора х, а дуга у, то его периметр
l и площадь S выразятся так (рис.24):
l = 2х + у,
S = xy:2 = [x(l - 2x)]:2.
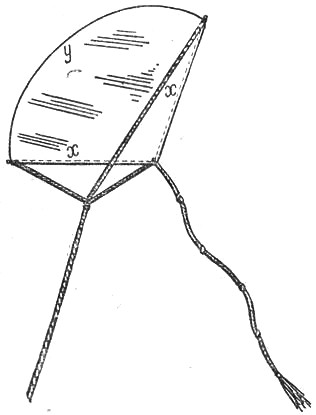
Рис. 24.
Величина
S достигает максимума при том же значении х, что и произведение 2х(l - 2x), т. е. учетверенная площадь. Так как сумма множителей 2x + (l - 2x) = l есть величина постоянная, то произведение их наибольшее, когда 2х = l - 2х, откуда
x = l/4,
y = l - 2 • l/4 = l/2.
Итак, сектор при данном периметре замыкает наибольшую площадь в том случае, когда его радиус составляет половину дуги (т. е. длина его дуги равна сумме радиусов или длина кривой части его периметра равна длине ломаной). Угол сектора равен ≈ 115°— двум радианам. Каковы летные качества такого широкого змея, — вопрос другой, рассмотрение которого в нашу задачу не входит.
З А Д А Ч А
На месте разрушенного дома, от которого уцелела одна стена, желают построить новый. Длина уцелевшей стены — 12 м. Площадь нового дома должна
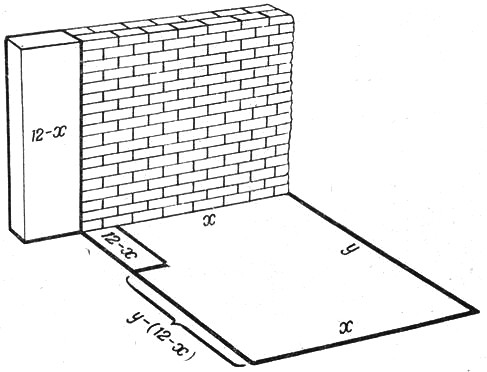
Рис. 25.
равняться 112 кв. м. Хозяйственные условия работы таковы:
1) ремонт погонного метра стены обходится в 25% стоимости кладки новой;
2) разбор погонного метра старой стены и кладка из полученного материала новой стены стоит 50% того, во что обходится постройка погонного метра стены из нового материала.
Как при таких условиях наивыгоднейшим образом использовать уцелевшую стену?
Р Е Ш Е Н И Е
Пусть от прежней стены сохраняется
x метров, а остальные 12 - х метров разбираются, чтобы из полученного материала возвести заново часть стены нового дома (рис. 25). Если стоимость кладки погонного метра стены из нового материала равна а, то ремонт х метров старой стены будет стоить ax:4; возведение участка длиной 12 - х будет стоить [a(12 - x)]:2; прочей части этой стены а[у - (12 - х)], т. е. а(y + х - 12); третьей стены ах, четвертой ау. Вся работа обойдется в
ax:4 + [a(12 - x)]:2 + a(y + x - 12) + ax + ay = [a(7x + 8y)]:4 - 6a.
Последнее выражение достигает наименьшей величины тогда же, когда и сумма
7х + 8у.
Мы знаем, что площадь дома ху равна 112; следовательно,
7х • 8у
- 56 • 112.
При постоянном произведении сумма 7х
+ 8у достигает наименьшей величины тогда, когда
7х = 8у,
откуда
y = 7/8x.
Подставив это выражение для у в уравнение
ху
= 112,
имеем:
![]()
А так как длина старой стены 12 м, то подлежит разборке только 0,7 м этой стены.
З А Д А Ч А
При постройке дачи нужно было отгородить дачный участок. Материала имелось на
l погонных метров изгороди. Кроме того, можно было воспользоваться ранее построенным забором (в качестве одной из сторон участка). Как при этих условиях отгородить прямоугольный участок наибольшей площади?
Р Е Ш Е Н И Е
Пусть длина участка (по забору) равна х, а ширина (т. е. размер участка в направлении, перпендикулярном к забору) равна у (рис. 26). Тогда для
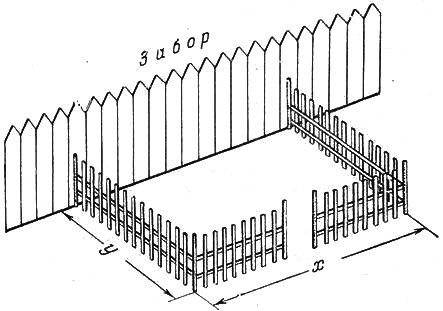
Рис. 26.
огораживания этого участка нужно х + 2у метров изгороди, так что
х + 2у =
l.
Площадь участка равна
S = xy = y(l -
2у).
Она принимает наибольшее значение одновременно с величиной
2у(
l - 2у)
(удвоенной площадью), которая представляет собой произведение двух множителей с постоянной суммой
l. Поэтому для достижения наибольшей площади должно быть
2у = 1 - 2у,
откуда
y = l/4, x = l - 2y = l/2.
Иначе говоря, х
= 2у, т. е. длина участка должна быть вдвое больше его ширины.
З
А Д А Ч А
Прямоугольный металлический лист (рис. 27) надо согнуть желобом с сечением в форме равнобокой трапеции. Это можно сделать различными способами,
|
|
|
|
|
Рис. 28. |
||
|
|
|
|
|
Рис. 27. |
Рис. 29. |
Рис. 30. |
как видно из рис. 28. Какой ширины должны быть боковые полосы и под каким углом они должны быть отогнуты, чтобы сечение желоба имело наибольшую площадь (рис. 29)?
Р Е Ш Е Н И Е
Пусть ширина листа l. Ширину отгибаемых боковых полос обозначим через х, а ширину дна желоба — через у. Введем еще одно неизвестное z, значение которого ясно из рис. 30.
Площадь трапеции, представляющей сечение желоба,
![]()
Задача свелась к определению тех значений х, у, z, при которых S достигает наибольшей величины; при этом сумма 2х + у (т. е. ширина листа) сохраняет постоянную величину l. Делаем преобразования:
S2
= (у + z)2(х + z)(х - z).
Величина S2 становится наибольшей при тех же значениях х, у, z, что и 3S2, последнюю же можно представить в виде произведения
(у + z)(y + z)(х + z)(3x - 3z).
Сумма этих четырех множителей
у + z + у + z + х + z + Зx - 3z = 2у + 4x = 2l,
т. е. неизменна. Поэтому произведение наших четырех множителей максимально, когда они равны между собой, т. е.
у + z = х + z и х + z = 3x - 3z.
Из первого уравнения имеем:
y = х,
а так как у + 2x = l, то х = у = l/3.
Из второго уравнения находим:
z = x/2 = l/6.
Далее, так как катет z равен половине гипотенузы x (рис. 30), то противолежащий этому катету угол равен 30°, а угол наклона боков желоба ко дну равен
90° + 30° = 120°.
Итак, желоб будет иметь наибольшее сечение, когда грани его согнуты в форме трех смежных сторон правильного шестиугольника.
З А Д А Ч А
Из жестяного круга нужно изготовить коническую часть воронки. Для этого в круге вырезают сектор и остальную часть круга свертывают конусом (рис. 31).
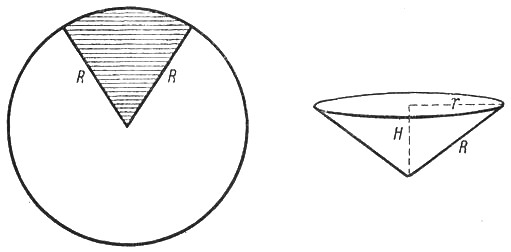
Рис. 31.
Сколько градусов должно быть в дуге вырезаемого сектора, чтобы конус получился наибольшей вместимости?
Р Е Ш Е Н И Е
Длину дуги той части круга, которая свертывается в конус, обозначим через х (в линейных мерах). Следовательно, образующей конуса будет радиус R жестяного круга, а окружность основания будет равна х. Радиус г основания конуса определяем из равенства
2πг = х, откуда г = x/2π.
Высота конуса (по теореме Пифагора)
![]()
(рис. 31). Объем этого конуса имеет значение
![]()
Это выражение достигает наибольшей величины одновременно с выражением
![]()
и его квадратом
(x:2π)4 : [R2 - (x:2π)2].
Так как
(x:2π)2 + R2 - (x:2π)2 = R2
есть величина постоянная, то последнее произведение имеет максимум при том значении х, когда
(x:2
π)2 : [R2 - (x:2π)2] = 2 : 1,
откуда
(x:2π)2 = 2R2 - 2(x:2π)2,
![]()
В градусах дуга х
≈ 295° и, значит, дуга вырезаемого сектора должна содержать ≈ 65°.
З А Д А Ч А
На какой высоте над столом должно находиться пламя свечи, чтобы всего ярче освещать лежащую на столе монету?
Р Е Ш Е Н И Е
Может показаться, что для достижения наилучшего освещения надо поместить пламя возможно ниже. Это неверно: при низком положении пламени лучи падают очень отлого. Поднять свечу так, чтобы лучи падали круто, — значит удалить источник света. Наиболее выгодна в смысле освещения, очевидно, некоторая средняя высота пламени над столом. Обозначим ее через х (рис. 32). Расстояние ВС монеты В от основания С перпендикуляра, проходящего через пламя A, обозначим через а. Если яркость пламени i, то

Рис. 32
освещенность монеты согласно законам оптики выразится так:
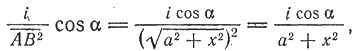
где a — угол падения пучка лучей АВ. Так как
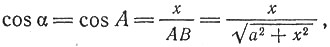
то освещенность равна
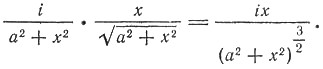
Это выражение достигает максимума при том же значении х, что и его квадрат, т. е.
i2x2 : (a2 + x2)3.
Множитель i2 как величину постоянную опускаем, а остальную часть исследуемого выражения преобразуем так:
x2 : (a2 + x2)3 = 1 : (x2 + a2)2 • [1 - a2 : (x2 + a2)] = [1 : (x2 + a2)]2 • [1 - a2 : (x2 + a2)].
Преобразованное выражение достигает максимума одновременно с выражением
[a2 : (x2 + a2)]2 • [1 - a2 : (x2 + a2)].
так как введенный постоянный множитель а4 не влияет на то значение х, при котором произведение достигает максимума. Замечая, что сумма первых степеней этих множителей
a2 : (x2 + a2) + [1 - a2 : (x2 + a2)] = 1
есть величина постоянная, заключаем, что рассматриваемое произведение становится наибольшим, когда
[a2 : (x2 + a2)] : [1 - a2 : (x2 + a2)] = 2 : 1
Имеем уравнение
а2
= 2х2 + 2а2 — 2а2.
Решив это уравнение, находим:
![]()
Монета освещается всего ярче, когда источник света находится на высоте 0,71 расстояния от проекции источника до монеты. Знание этого соотношения помогает при устройстве наилучшего освещения рабочего места.