

Язык алгебры
Искусство составлять уравнения
Язык алгебры — уравнения. «Чтобы решить вопрос, относящийся к числам или к отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», — писал великий Ныотон в своем учебнике алгебры, озаглавленном «Всеобщая арифметика». Как именно выполняется такой перевод с родного языка на алгебраический, Ныотон показал на примерах. Вот один из них:

| На родном языке: | На языке алгебры: |
|
Купец имел некоторую сумму денег. |
X |
|
В первый год он истратил 100 фунтов. |
x - 100 |
|
К оставшейся сумме добавил третью ее часть. |
(x - 100) + (x - 100)/3 = (4x - 400)/3 |
|
В следующем году он вновь истратил 100 фунтов |
(4х — 400)/3 - 100 = (4х — 700)/3 |
|
и увеличил оставшуюся сумму на третью ее часть. |
(4х — 700)/3 + (4x - 700)/9 = (16x - 2800)/9 |
|
В третьем году он опять истратил 100 фунтов. |
(16x - 2800)/9 - 100 = (16x - 3700)/9 |
|
После того как он добавил к остатку третью его часть. |
(16x - 3700)/9 + (16x - 3700)/27 = (64x - 14800)/27 |
|
капитал его стал вдвое больше первоначального. |
|
Чтобы определить первоначальный капитал купца, остается только решить последнее уравнение.
Решение уравнений
— зачастую дело нетрудное; составление уравнений по данным задачи затрудняет больше. Вы видели сейчас, что искусство составлять уравнения действительно сводится к умению переводить «с родного языка на алгебраический». Но язык алгебры весьма немногословен; поэтому перевести на него удается без труда далеко не каждый оборот родной речи. Переводы попадаются различные по трудности, как убедится читатель из ряда приведенных далее примеров на составление уравнений первой степени.
З А Д А Ч А
История сохранила нам мало черт биографии замечательного древнего математика Диофанта. Все, что известно о нем, почерпнуто из надписи на его гробнице — надписи, составленной в форме математической задачи. Мы приведем эту надпись.
|
На родном языке: |
На языке алгебры: |
|
Путник! Здесь прах погребен Диофанта. И числа поведать Могут, о чудо, сколь долог был век его жизни. |
X |
|
Часть шестую его представляло прекрасное детство. |
X/6 |
| Двенадцатая часть протекла еще жизни — покрылся Пухом тогда подбородок. | X/12 |
| Седьмую в бездетном Браке провел Диофант. | X/7 |
| Прошло пятилетие; он Был осчастливен рожденьем прекрасного первенца сына, | 5 |
| Коему рок половину лишь жизни прекрасной и светлой Дал на земле по сравненью с отцом. | Х/2 |
| И в печали глубокой Старец земного удела конец восприял, переживши Года четыре с тех пор, как сына лишился. | Х = х/6 + х/12 + х/7 + 5 + х/2 + 4 |
|
Скажи, сколько лет жизни достигнув, Смерть восприял Диофант? |
|
Р Е Ш Е Н И Е
Решив уравнение и найдя, что х = 84, узнаем следующие черты биографии Диофанта; он женился 21 года, стал отцом на 38-м году, потерял сына на 80-м году и умер 84 лет.
З А Д А Ч А
Вот еще несложная старинная задача, легко переводимая с родного языка на язык алгебры.
«Лошадь и мул шли бок о бок с тяжелой поклажей на спине. Лошадь жаловалась на свою непомерно тяжелую ношу. «Чего ты жалуешься? — отвечал ей мул. — Ведь если я возьму у тебя один мешок, ноша моя станет вдвое тяжелее твоей. А вот если бы ты сняла с моей спины один мешок, твоя поклажа стала бы одинакова с моей».
Скажите же, мудрые математики, сколько мешков несла лошадь и сколько нес мул?».
Р Е Ш Е Н И Е
|
Если я возьму у тебя один мешок, |
х - 1 |
|
ноша моя |
У + 1 |
|
станет вдвое тяжелее твоей. |
у + 1 — 2(х — 1) |
|
А вот если бы ты сняла с моей спины один мешок, |
у - 1 |
|
твоя поклажа |
х + 1 |
|
стала бы одинакова с моей. |
у - 1 = х + 1 |
Мы привели задачу к системе уравнений с двумя неизвестными:
| у + 1 = 2(х - 1) | } | или | { | 2х - у = 3 |
| у - 1 = х + 1 | у - х = 2 |
Решив ее, находим: х = 5, у = 7. Лошадь несла 5 мешков и 7 мешков — мул.
З А Д А Ч А
У четырех братьев 45 рублей. Если деньги первого увеличить на 2 рубля, деньги второго уменьшить на 2 рубля, деньги третьего увеличить вдвое, а деньги четвертого уменьшить вдвое, то у всех окажется поровну. Сколько было у каждого?
Р Е Ш Е Н И Е
|
У четырех братьев 45 руб. |
x + y + z + t = 45 |
|
Если деньги первого увеличить на 2 руб., |
x + 2 |
|
деньги второго уменьшить на 2 руб., |
y - 2 |
|
деньги третьего увеличить вдвое, |
2z |
|
деньги четвертого уменьшить вдвое, |
t/2 |
|
то у всех окажется поровну. |
x + 2 = y - 2 = 2z = t/2 |
Расчленяем последнее уравнение на три отдельных!
х + 2 = у — 2,
х
+ 2 = 2z,х
+ 2 = t/2,
откуда
у = х + 4,
z = (х + 2)/2,
t = 2x+ 4.
Подставив эти значения в первое уравнение, получаем:
x + x + 4 + (x + 2а)/2 + 2x + 4 = 45,
откуда х = 8
. Далее находим: у = 12, z = 5, t = 20.Итак, у братьев было:
8 руб., 12 руб., 5 руб., 20 руб.
З А Д А Ч А
У одного арабского математика XI века находим следующую задачу.
На обоих берегах реки растет по пальме, одна против другой. Высота одной — 30 локтей, другой — 20 локтей; расстояние между их основаниями — 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами; они кинулись к ней разом и достигли ее одновременно.

Рис. 4.
На каком расстоянии от основания более высокой пальмы появилась рыба?
Р Е Ш Е Н И Е
Из схематического чертежа (рис. 5), пользуясь теоремой Пифагора, устанавливаем:
АВ2 = З02 + х2, АС2 = 202 + (50 — х)2.
Но АВ = АС, так как обе птицы пролетели эти расстояния в одинаковое время. Поэтому
302 + х2 = 202 + (50 — х)2.
Раскрыв скобки и сделав упрощения, получаем уравнение первой степени
100х = 2000, откуда х = 20.
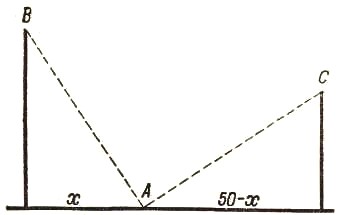
Рис. 5.
Рыба появилась в 20 локтях от той пальмы, высота которой 30 локтей.
З А Д А Ч А
— Зайдите ко мне завтра днем, — сказал старый доктор своему знакомому.
— Благодарю вас. Я выйду в три часа. Может быть, и вы надумаете прогуляться, так выходите в то же время, встретимся на полпути.
— Вы забываете, что я старик, шагаю в час всего только 3 км, а вы, молодой человек, проходите при самом медленном шаге 4 км в час. Не грешно бы дать мне небольшую льготу.
— Справедливо. Так как я прохожу больше вас на 1 км в час, то, чтобы уравнять нас, дам вам этот километр, т. е. выйду на четверть часа раньше. Достаточно?
— Очень любезно с вашей стороны, — поспешил согласиться старик.
Молодой человек так и сделал: вышел из дому в три четверти третьего и шел со скоростью 4 км в час. А доктор вышел ровно в три и делал по 3 км в час. Когда они встретились, старик повернул обратно и направился домой вместе с молодым другом.
Только возвратившись к себе домой, сообразил молодой человек, что из-за льготной четверти часа ему пришлось в общем итоге пройти не вдвое, а вчетверо больше, чем доктору.
Как далеко от дома доктора до дома его молодого знакомого?
Р Е Ш Е Н И Е
Обозначим расстояние между домами через х (км). Молодой человек всего прошел 2х, а доктор вчетверо меньше, т. е. х/2. До встречи доктор прошел половину пройденного им пути, т. е. х/4, а молодой человек — остальное, т. е. 3х/4. Свою часть пути доктор прошел в х/12 часа, а молодой человек - в 3х/16 часа, причем мы знаем, что он был в пути на 1/4 часа дольше, чем доктор.
Имеем уравнение
3х/16 - х/12 = 1/4,
откуда х = 2,4 км.
От дома молодого человека до дома доктора 2,4 км.
Известный физик А. В. Цингер в своих воспоминаниях о Л. Н. Толстом рассказывает о следующей задаче, которая очень нравилась великому писателю:
«Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и
докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался

Рис. 6.
участок, скошенный на другой день одним косцом за один день работы.
Сколько косцов было в артели?».
Р
Е Ш Е Н И Е
В этом случае, кроме главного неизвестного — числа косцов, которое мы обозначим через х, — удобно ввести еще и вспомогательное, именно — размер участка, скашиваемого одним косцом в 1 день; обозначим его через у. Хотя задача и не требует его определения, оно облегчит нам нахождение главного неизвестного.
Выразим через х и у площадь большого луга. Луг этот косили полдня х косцов; они скосили
х • 1/2 • у = ху/2.
Вторую половину дня его косила только половина артели, т. е. х/2 — косцов; они скосили
х/2 • 1/2 • у = ху/4.
Так как к вечеру скошен был весь луг, то площадь его равна
ху/2 + ху/4 = 3ху/4.
Выразим теперь через х и у площадь меньшего луга. Его полдня косили х/2 косцов и скосили площадь х/2 • 1/2 • у = ху/4. Прибавим недоношенный участок, как раз равный у (площади, скашиваемой одним косцом в 1 рабочий день), и получим площадь меньшего луга:
ху/4 + у = (ху + 4у)/4.
Остается перевести на язык алгебры фразу: «первый луг вдвое больше второго», — и уравнение составлено:
3ху/4 : (ху + 4у)/4 = 2, или 3ху/(ху + 4у) = 2.
Сократим дробь в левой части уравнения на у; вспомогательное неизвестное благодаря этому исключается, и уравнение принимает вид
3х/(х + 4) = 2, или 3х = 2х + 8,
откуда х = 8.
В артели было 8 косцов.
После напечатания первого издания «Занимательной алгебры» проф. А. В. Цингер прислал мне подробное и весьма интересное сообщение, касающееся этой задачи. Главный эффект задачи, по его мнению, в том, что «она совсем не алгебраическая, а арифметическая и притом крайне простая, затрудняющая только своей нешаблонной формой».
«История этой задачи такова, — продолжает проф. А. В. Цингер. — В Московском университете на математическом факультете в те времена, когда там учились мой отец и мой дядя И. И. Раевский (близкий друг Л. Толстого), среди прочих предметов преподавалось нечто вроде педагогики. Для этой цели студенты должны были посещать отведенную для университета городскую народную школу и там в сотрудничестве с опытными искусными учителями упражняться в преподавании. Среди товарищей Цингера и Раевского был некий студент Петров, по рассказам — чрезвычайно одаренный и оригинальный человек. Этот Петров (умерший очень молодым, кажется, от чахотки) утверждал, что на уроках арифметики учеников портят, приучая их к шаблонным задачам и к шаблонным способам решения. Для подтверждения своей мысли Петров изобретал задачи, которые вследствие нешаблонности очень затрудняли «опытных искусных учителей», но легко решались более способными учениками, еще не испорченными учебой. К числу таких задач (их Петров сочинил несколько) относится и задача об артели косцов. Опытные учителя, разумеется, легко могли решать ее при помощи уравнения, но простое арифметическое решение от них ускользало. Между тем, задача настолько проста, что привлекать для ее решения алгебраический аппарат совсем не стоит.
| 1/3 | |
| 1/3 | |
|
1/6 |
|
| 1/3 |
1/3 |
Рис. 7.
Если большой луг полдня косила вся артель и полдня пол-артели, то ясно, что в полдня пол-артели скашивает 1/3 луга. Следовательно, на малом лугу остался нескошенным участок в 1/2 - 1/3 = 1/6. Если один косец в день скашивает
1/6 луга, а скошено было 6/6 + 2/6 = 8/6, то косцов было 8.Толстой, всю жизнь любивший фокусные, не слишком хитрые задачи. Когда об этой задаче беседовали с Толстым — уже стариком, его особенно восхитило то, что задача делается гораздо яснее и прозрачнее, если при решении пользоваться самым примитивным чертежом (рис. 7)».
Ниже нам встретятся еще несколько задач, которые при некоторой сообразительности проще решаются арифметически, чем алгебраически.
З А Д А Ч А
«При изучении наук задачи полезнее правил», — писал Ньютон в своей «Всеобщей арифметике» и сопровождал теоретические указания рядом примеров.
В числе этих упражнений находим задачу о быках, пасущихся на лугу, — родоначальницу особого типа своеобразных задач наподобие следующей.
«Трава на всем лугу растет одинаково густо и быстро. Известно, что 70 коров поели бы ее в 24 дня, а 30 коров — в 60 дней. Сколько коров поели бы всю траву луга в 96 дней?».

Рис. 8.
Задача эта послужила сюжетом для юмористического рассказа, напоминающего чеховский «Репетитор». Двое взрослых, родственники школьника, которому эту задачу задали для решения, безуспешно трудятся над нею и недоумевают:
— Выходит что-то странное, — говорит один из решающих: — если в 24 дня 70 коров поедают всю траву луга, то сколько коров съедят ее в 96 дней? Конечно, 1/4 от 70, т.е. 17,5 коров... Первая нелепость! А вот вторая: 30 коров поедают траву в 60 дней; сколько коров съедят ее в 96 дней? Получается еще хуже 183/4 коровы. Кроме того: если 70 коров поедают траву в 24 дня, то 30 коров употребляют на это 56 дней, а вовсе не 60, как утверждает задача.
— А приняли вы в расчет, что трава все время растет? — спрашивает другой.
Замечание резонное: трава непрерывно растет, и если этого не учитывать, то не только нельзя решить задачи, но и само условие ее будет казаться противоречивым.
Как же решается задача?
Р Е Ш Е Н И Е
Введем и здесь вспомогательное неизвестное, которое будет обозначать суточный прирост травы в долях ее запаса на лугу. В одни сутки прирастает у.
в 24 дня — 24у; если общий запас принять за 1, то в течение 24 дней коровы съедают
1 + 24 у.
В сутки все стадо (из 70 коров) съедает
(1 + 24у)/24.
а одна корова съедает
(1 + 24у)/24
• 70.
Подобным же образом из того, что 30 коров поели бы траву того же луга в 60 суток, выводим, что одна корова съедает в сутки
(1 + 60у)/30 • 60.
Но количество травы, съедаемое коровой в сутки, для обоих стад одинаково. Поэтому
(1 + 24у)/24
• 70 = (1 + 60у)/30 • 60,
откуда
у = 1/480.
Найдя у (величину прироста), легко уже определить, какую долю первоначального запаса травы съедает одна корова в сутки;
(1 + 24у)/24 • 70 = (1 + 24
• 1/480)/24 • 70 = 1/1600.
Наконец, составляем уравнение для окончательного решения задачи: если искомое число коров х, то
(1 + 96
• 1/480)/96х = 1/1600.
откуда х = 20.
20 коров поели бы всю траву в 96 дней.
Рассмотрим теперь ньютонову задачу о быках, по образцу которой составлена сейчас рассмотренная.
Задача, впрочем, придумана не самим Ньютоном; она является продуктом народного математического творчества.
«Три луга, покрытые травой одинаковой густоты и скорости роста, имеют площади: 3
1/3 га, 10 га и 24 га. Первый прокормил 12 быков в продолжение 4 недель; второй — 21 быка в течение 9 недель. Сколько быков может прокормить третий луг в течение 18 недель?».
Р Е Ш Е Н И Е
Введем вспомогательное неизвестное у, означающее, какая доля первоначального запаса травы прирастает на 1 га в течение недели. На первом лугу в течение недели прирастает травы 31/3у, а в течение 4 недель 31/3у • 4 = 40/3у того запаса, который первоначально имелся на 1 га. Это равносильно тому, как если бы первоначальная площадь луга увеличилась и сделалась равной
(31/3 + 40/3у)
гектаров. Другими словами, быки съели столько травы, сколько покрывает луг площадью в 31/3 + 40/3у гектаров. В одну неделю 12 быков поели четвертую часть этого количества, а 1 бык в неделю часть, т, е, запас, имеющийся на площади
(31/3 + 40у/3) : 48 = (10 + 40у)/144
гектаров.
Подобным же образом находим площадь луга, кормящего одного быка в течение недели, из данных для второго луга:
недельный прирост на 1 га = у,
9-недельный прирост на 1 га = 9у,
9-недельный прирост на 10 га = 90у.
Площадь участка, содержащего запас травы для прокормления 21 быка в течение 9 недель, равна
10 + 90у.
Площадь, достаточная для прокормления 1 быка в течение недели, —
(10 + 90у) : 9
• 21 = (10 + 90у) : 189
гектаров. Обе нормы прокормления должны быть одинаковы:
(10 + 40у) : 144 = (10 + 90у) : 189.
Решив это уравнение, находим у = 1/12.
Определим теперь площадь луга, наличный запас травы которого достаточен для прокормления одного быка в течение недели:
(10 + 40у) : 144 = (10 + 40 • 1/12) : 144 = 5/54
гектаров. Наконец, приступаем к вопросу задачи. Обозначив искомое число быков через х, имеем:
(24 + 24 • 18 • 1/12) : 18х = 5/54,
откуда х = 36. Третий луг может прокормить в течение 18 недель 36 быков.
З А Д А Ч А
Биограф и друг известного физика А. Эйнштейна А. Мошковский, желая однажды развлечь своего приятеля во время болезни, предложил ему следующую задачу (рис. 9):
«Возьмем, — сказал Мошковский, — положение стрелок в 12 часов. Если бы в этом положении большая и малая стрелки обменялись местами, они дали бы все же правильные показания. Но в другие моменты, — например, в 6 часов, взаимный обмен стрелок привел бы к абсурду, к положению, какого на правильно идущих часах быть не может: минутная стрелка не может стоять на 6, когда часовая показывает 12. Возникает вопрос: когда и как часто стрелки часов занимают такие положения, что замена одной другою дает новое положение, тоже возможное на правильных часах?
— Да, — ответил Эйнштейн, — это вполне подходящая задача для человека, вынужденного из-за болезни оставаться в постели: достаточно интересная и не слишком легкая. Боюсь только, что развлечение продлится недолго: я уже напал на путь к решению.
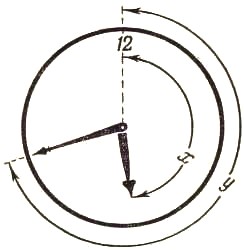
Рис. 9.
И приподнявшись на постели, он несколькими штрихами набросал на бумаге схему, изображающую условие задачи. Для решения ему понадобилось не больше времени, чем мне на формулировку задачи...»
Как же решается эта задача?
Р Е Ш Е Н И Е
Будем измерять расстояния стрелок по кругу циферблата от точки, где стоит цифра 12, в 60-х долях окружности.
Пусть одно из требуемых положений стрелок наблюдалось тогда, когда часовая стрелка отошла от цифры 12 на х делений, а минутная — на у делений. Так как часовая стрелка проходит 60 делений за 12 часов, т. е. 5 делений в час, то х делений она прошла за х/5 часов. Иначе говоря, после того как часы показывали 12, прошло х/5 часов.
Минутная стрелка прошла у делений за у минут, т. е. за у/60 часов. Иначе говоря, цифру 12 минутная стрелка прошла у/60 часов тому назад, или через
х/5 - у/60
часов после того, как обе стрелки были на двенадцати. Это число является целым (от нуля до 11)
, так как оно показывает, сколько полных часов прошло после двенадцати.Когда стрелки обменяются местами, мы найдем аналогично, что с двенадцати часов до времени, показываемого стрелками, прошло
y/5 - x/60
полных часов. Это число также является целым (от нуля до 11).
Имеем систему уравнений
|
{ |
х/5 - у/60 = m |
| у/5 - х/60 = n |
где m и n — целые числа, которые могут меняться от 0 до 11. Из этой системы находим:
х = 60(12m + n) : 143,
у = 60(12n + m) : 143.
Давая m и n значения от 0 до 11, мы определим все требуемые положения стрелок. Так как каждое из 12 значений m можно сопоставлять с каждым из 12 значений n, то, казалось бы, число всех решений равно 12 • 12 = 144. Но в действительности оно равно 143, потому что при m = 0, n = 0 и при m = 11, n = 11 получается одно и то же положение стрелок.
При m = 11, n = 11 имеем:
х = 60, у = 60,
т. е. часы показывают 12, как и в случае m = 0, n = 0.
Всех возможных положений мы рассматривать не станем; возьмем лишь два примера.
Первый пример:
m =
1, n = 1;х = 60 • 13 : 143 = 55/11, у = 55/11,
т. е. часы показывают 1 час 55/11 мин.; в этот момент стрелки совмещаются; их, конечно, можно обменять местами (как и при всех других совмещениях стрелок).
Второй пример:
m = 8, n = 5;
x = 60(5 + 12
• 8) : 143 ≈ 42.38, y = 90(8 + 12 • 5) : 143 ≈ 28.53.
Соответствующие моменты: 8 час. 28,53 мин. и 5 час. 42,38 мин.
Число решений мы знаем: 143. Чтобы найти все точки циферблата, которые дают требуемые положения стрелок, надо окружность циферблата разделить на 143 равные части: получим 143 точки, являющиеся искомыми. В промежуточных точках требуемые положения стрелок невозможны.
З А Д А Ч А
Сколько есть положений на правильно идущих часах, когда часовая и минутная стрелка совмещаются?
Р Е Ш Е Н И Е
Мы можем воспользоваться уравнениями, выведенными при решении предыдущей задачи: ведь если часовая и минутная стрелка совместились, то их можно обменять местами — от этого ничего не изменится. При этом обе стрелки прошли одинаковое число делений от цифры 12, т. е. х = у. Таким образом, из рассуждений, относящихся к предыдущей задаче, мы выводим уравнение
х/5 - х/60 =
m,
где
m — целое число от 0 до 11. Из этого уравнения находим:
х = 60
m/11.
Из двенадцати возможных значений для
m (от нуля до 11) мы получаем не 12, а только 11 различных положений стрелок, так как при m = 11 мы находим х = 60, т. е. обе стрелки прошли 60 делений и находятся на цифре 12; это же получается при m = 0.
Каждый из вас, несомненно, встречался с «фокусами» по отгадыванию чисел. Фокусник обычно предлагает выполнить действия следующего характера: задумай число, прибавь 2, умножь на 3, отними 5, отними задуманное число и т. д. — всего пяток, а то и десяток действий. Затем фокусник спрашивает, что у вас получилось в результате, и, получив ответ, мгновенно сообщает задуманное вами число.
Секрет «фокуса», разумеется, очень прост, и в основе его лежат все те же уравнения.
Пусть, например, фокусник предложил вам выполнить программу действий, указанную в левой колонке следующей таблицы:
|
Задумай число, |
X |
|
прибавь 2, |
х + 2 |
|
умножь результат на 3, |
Зх + 6 |
|
отними 5, |
Зх + 1 |
|
отними задуманное число, |
2х+ 1 |
|
умножь на 2, |
4х + 2 |
|
отними 1 |
4х+ 1 |
Затем фокусник просит вас сообщить окончательный результат и, получив его, моментально называет задуманное число. Как он это делает?
Чтобы понять это, достаточно обратиться к правой колонке таблицы, где указания фокусника переведены на язык алгебры. Из этой колонки видно, что если вы задумали какое-то число х, то после всех действий у вас должно получиться 4х + 1. Зная это, нетрудно «отгадать» задуманное число.
Пусть, например, вы сообщили фокуснику, что получилось 33. Тогда фокусник быстро решает в уме уравнение 4х + 1 = 33 и находит: х = 8. Иными словами, от окончательного результата надо отнять единицу (33 — 1 = 32) и затем полученное число разделить на 4 (32:4 = 8); это и дает задуманное число (8). Если же у вас получилось 25, то фокусник в уме проделывает действия 25 — 1 = 24, 24 : 4 = 6 и сообщает вам, что вы задумали 6.
Как видите, все очень просто: фокусник заранее знает, что надо сделать с результатом, чтобы получить задуманное число.
Поняв это, вы можете еще более удивить и озадачить ваших приятелей, предложив им самим, по своему усмотрению, выбрать характер действий над задуманным числом. Вы предлагаете приятелю задумать число и производить в любом порядке действия следующего характера: прибавлять или отнимать известное число (скажем: прибавить 2, отнять 5 и т. д.), умножать на известное число (на 2, на 3 и т. п.), прибавлять или отнимать задуманное число. Ваш приятель нагромождает, чтобы запутать вас, ряд действий. Например, он задумывает число 5 (этого он вам не сообщает) и, выполняя действия, говорит:
— Я задумал число, умножил его на 2, прибавил к результату 3, затем прибавил задуманное число; теперь я прибавил 1, умножил на 2, отнял задуманное число, отнял 3, еще отнял задуманное число, отнял 2. Наконец, я умножил результат на 2 и прибавил 3.
Решив, что он уже совершенно вас запутал, он с торжествующим видом сообщает вам:
— Получилось 49.
К его изумлению вы немедленно сообщаете ему, что он задумал число 5.
Как вы это делаете? Теперь это уже достаточно ясно. Когда ваш приятель сообщает вам о действиях, которые он выполняет над задуманным числом, вы одновременно действуете в уме с неизвестным
х. Он вам говорит: «Я задумал число...», а вы про себя твердите: «значит, у нас есть х». Он говорит: «...умножил его на 2...» (и он в самом деле производит умножение чисел), а вы про себя продолжаете: «теперь 2х». Он говорит: «...прибавил к результату 3...», и вы немедленно следите: 2х + 3, и т. д. Когда он «запутал» вас окончательно и выполнил все те действия, которые перечислены выше, у вас получилось то, что указано в следующей таблице (левая колонка содержит то, что вслух говорит ваш приятель, а правая — те действия, которые вы выполняете в уме):
|
Я задумал число, |
X |
|
умножил его на 2, |
2х |
|
прибавил к результату 3, |
2х + 3 |
|
затем прибавил задуманное число, |
Зх + 3 |
|
теперь я прибавил 1, |
3.x+ 4 |
|
умножил на 2, |
бх + 8 |
|
отнял задуманное число, |
5*+ 8 |
|
отнял 3, |
5х + 5 |
|
еще отнял задуманное число, |
4х + 5 |
|
отнял 2, |
4х + 3 |
|
наконец, я умножил результат на 2 |
8х + 6 |
|
и прибавил 3 |
8х + 9 |
В конце концов вы про себя подумали: окончательный результат 8х + 9. Теперь он говорит: «У меня получилось 49». А у вас готово уравнение:
8х + 9 = 49. Решить его—пара пустяков, и вы немедленно сообщаете ему, что он задумал число 5.Фокус этот особенно эффектен потому, что не вы предлагаете те операции, которые надо произвести над задуманным числом, а сам товарищ ваш «изобретает» их.
Есть, правда, один случай, когда фокус не удается. Если, например, после ряда операций вы (считая про себя) получили
х = 14, а затем ваш товарищ говорит: «...теперь я отнял задуманное число; у меня получилось 14», то вы следите за ним: (х + 14) — х = 14 — в самом деле получилось 14, но никакого уравнения нет и отгадать задуманное число вы не в состоянии. Что же в таком случае делать? Поступайте так: как только у вас получается результат, не содержащий неизвестного х, вы прерываете товарища словами: «Стоп! Теперь я могу, ничего не опрашивая, сказать, сколько у тебя получилось: у тебя 14». Это уже совсем озадачит вашего приятеля — ведь он совсем ничего вам не говорил! И, хотя вы так и не узнали задуманное число, фокус получился на славу!Вот пример (по-прежнему в левой колонке стоит то, что говорит ваш приятель):
|
Я задумал число, |
X |
|
прибавил к нему 2 |
х + 2 |
|
и результат умножил на 2, |
2х + 4 |
|
теперь я прибавил 3, |
2х + 7 |
|
отнял задуманное число, |
х + 7 |
|
прибавил 5, |
х + 12 |
|
затем я отнял задуманное число... |
12 |
В тот момент, когда у вас получилось число 12, т. е. выражение, не содержащее больше неизвестного
х, вы и прерываете товарища, сообщив ему, что теперь у него получилось 12.Немного поупражнявшись, вы легко сможете показывать своим приятелям такие «фокусы».
З А Д А Ч А
Вот задача, которая может показаться совершенно абсурдной:
Чему равно 84, если 8 • 8 = 54?
Этот странный вопрос далеко не лишен смысла, и задача может быть решена с помощью уравнений.
Попробуйте расшифровать ее.
РЕШЕНИЕ
Вы догадались, вероятно, что числа, входящие в задачу, написаны не по десятичной системе, — иначе вопрос «чему равно 84» был бы нелепым. Пусть основание неизвестной системы счисления есть х. Число «84» означает тогда 8 единиц второго разряда и 4 единицы первого, т. е.
«84» = 8х + 4.
Число «54» означает 5х + 4.
Имеем уравнение 8 • 8 = 5х + 4, т. е. в десятичной системе 64 = 5х + 4, откуда х = 12.
Числа написаны по двенадцатеричной системе, и «84» = 8 • 12 + 4 = 100. Значит, если 8 • 8 = «54», то «84» = 100.
Подобным же образом решается и другая задача в этом роде:
Чему равно 100, когда 5 • 6 = 33?
Ответ: 81 (девятеричная система счисления).
Если вы сомневаетесь в том, что уравнение бывает иной раз предусмотрительнее нас самих, решите следующую задачу:
Отцу 32 года, сыну 5 лет. Через сколько лет отец будет в 10 раз старше сына?
Обозначим искомый срок через х. Спустя х лет, отцу будет 32 + х лет, сыну 5 + х. И так как отец должен тогда быть в 10 раз старше сына, то имеем уравнение
32 + х = 10(5 + х).
Решив его, получаем х = — 2.
«Через минус 2 года» означает «два года назад». Когда мы составляли уравнение, мы не подумали о том, что возраст отца никогда в будущем не окажется в 10 раз превосходящим возраст сына — такое соотношение могло быть только в прошлом. Уравнение оказалось вдумчивее нас и напомнило о сделанном упущении.
При решении уравнений мы наталкиваемся иногда на ответы, которые могут поставить в тупик малоопытного математика. Приведем несколько примеров.
I.
Найти двузначное число, обладающее следующими свойствами. Цифра десятков на 4 меньше цифры единиц. Если из числа, записанного теми же цифрами, но в обратном порядке, вычесть искомое число, то получится 27.Обозначив цифру десятков через х, а цифру единиц — через у, мы легко составим систему уравнений для этой задачи:
|
{ |
х = у - 4, |
| (10у + х) - (10х + у) = 27. |
Подставив во второе уравнение значение х из первого, найдем:
10у + у - 4 - [10(у — 4) + у] = 27,
а после преобразований:
36 = 27.
У нас не определились значения неизвестных, зато мы узнали, что 36 = 27... Что это значит?
Это означает лишь, что двузначного числа, удовлетворяющего поставленным условиям, не существует
и что составленные уравнения противоречат одно другому.В самом деле: умножив обе части первого уравнения на 9, мы найдем из него:
9
у — 9х = 36,
а из второго (после раскрытия скобок и приведения подобных членов):
9
у — 9х = 27.
Одна и та же величина 9
у — 9х согласно первому уравнению равна 36, а согласно второму 27. Это безусловно невозможно, так как 36 ≠ 27.Подобное же недоразумение ожидает решающего следующую систему уравнений:
|
{ |
х2у2 = 8, |
| ху = 4. |
Разделив первое уравнение на второе, получаем:
ху = 2,
а сопоставляя полученное уравнение со вторым, видим, что
|
{ |
ху = 4, |
| ху = 2, |
т. е. 4 = 2. Чисел, удовлетворяющих этой системе, не существует. (Системы уравнений, которые, подобно сейчас рассмотренным, не имеют решений, называются несовместными.)
II. С иного рода неожиданностью встретимся мы, если несколько изменим условие предыдущей задачи. Именно будем считать, что цифра десятков не на 4, а на 3 меньше, чем цифра единиц, а в остальном оставим условие задачи тем же. Что это за число?
Составляем уравнение. Если цифру десятков обозначим через
х, то число единиц выразится через х + 3. Переводя задачу на язык алгебры, получим:
10
(х + 3) + х — [10х + (х + 3)] = 27.
Сделав упрощения, приходим к равенству
27 = 27.
Это равенство неоспоримо верно, но оно ничего не говорит нам о значении
х. Значит ли это, что чисел, удовлетворяющих требованию задачи, не существует?Напротив, это означает, что составленное нами уравнение есть тождество, т. е. что оно верно при любом значении неизвестного
х. Действительно, легко убедиться в том, что указанным в задаче свойством обладает каждое двузначное число, у которого цифра единиц на 3 больше цифры десятков:
14 + 27 = 41, 47 + 27 = 74,
25 + 27 = 52, 58 + 27 = 85,
36 + 27 = 63, 69 + 27 = 96.
III. Найти трехзначное число, обладающее следующими свойствами:
1) цифра десятков 7;
2) цифра сотен на 4 меньше цифры единиц;
3) если цифры этого числа разместить в обратном порядке, то новое число будет на 396 больше искомого.
Составим уравнение, обозначив цифру единиц через
х:
100х + 70 + х - 4 - [100
(х - 4) + 70 + х] = 396.
Уравнение это после упрощений приводит к равенству
396 = 396.
Читатели уже знают, как надо толковать подобный результат. Он означает, что каждое трехзначное число, в котором первая цифра на 4 меньше третьей, увеличивается на 396, если цифры поставить в обратном порядке.
До сих пор мы рассматривали задачи, имеющие более или менее искусственный, книжный характер; их назначение — помочь приобрести навык в составлении и решении уравнений. Теперь, вооруженные теоретически, займемся несколькими примерами задач практических— и з области производства, обихода, военного дела, спорта.
З
А Д А Ч А
Может ли алгебра понадобиться в парикмахерской? Оказывается, что такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:
— Не поможете ли нам разрешить задачу, с которой мы никак не справимся?
— Уж сколько раствора испортили из-за этого! — добавил другой.
— В чем задача? — осведомился я.
— У нас имеется два раствора перекиси водорода: 30-процентный и 3-процентный. Нужно их смешать так, чтобы составился 12-процентный раствор. Не можем подыскать правильной пропорции...
Мне дали бумажку, и требуемая пропорция была найдена.
Она оказалась очень простой. Какой именно?
Р
Е Ш Е Н И Е
Задачу можно решить и арифметически, но язык алгебры приводит здесь к цели проще и быстрее. Пусть для составления 12-процентной смеси требуется взять х граммов 3-процентного раствора и у граммов 30-процентного. Тогда в первой порции содержится 0,03х граммов чистой перекиси водорода, во второй 0,3у, а всего
0,03х + 0,3у.
В результате получается (х + у) граммов раствора, в котором чистой перекиси должно быть 0,12(x + у).
Имеем уравнение
0,03х + 0,3у = 0,12(х + у).
Из этого уравнения находим х = 2у, т. е. 3-процентного раствора надо взять вдвое больше, чем 30-процентного.
З А Д А Ч А
Идя вдоль трамвайного пути, я заметил, что каждые 12 минут меня нагоняет трамвай, а каждые 4 минуты я сам встречаю трамвай. И я и трамваи движемся равномерно.
Через сколько минут один после другого покидают трамвайные вагоны свои конечные пункты?
Р Е Ш Е Н И Е
Если вагоны покидают свои конечные пункты каждые х минут, то это означает, что в то место, где я встретился с одним из трамваев, через х минут приходит следующий трамвай. Если он догоняет меня, то в оставшиеся 12 — х минут он должен пройти тот путь, который я успеваю пройти в 12 минут. Значит, тот путь, который я прохожу в 1 минуту, трамвай проходит в (12 — х) : 12 минут.
Если же трамвай идет мне навстречу, то он встретит меня через 4 минуты после предыдущего, а в оставшиеся (х — 4) минуты он пройдет тот путь, который я успел пройти в эти 4 минуты. Следовательно, тот путь, который я прохожу в 1 минуту, трамвай проходит в (х — 4) : 4 минуты.
Получаем уравнение
(12 - х) : 12 = (х - 4) : 4.
Отсюда х = 6. Вагоны отходят каждые 6 минут. Можно также предложить следующее (по сути дела арифметическое) решение задачи. Обозначим расстояние между двумя следующими один за другим трамваями через а. Тогда между мной и трамваем, двигающимся навстречу, расстояние уменьшается на а/4 в минуту (так как расстояние между только что прошедшим трамваем и следующим, равное а, мы вместе проходим за 4 минуты). Если же трамвай догоняет меня, то расстояние между нами ежеминутно уменьшается на а/12. Предположим теперь, что я в течение минуты шел вперед, а затем повернул назад и минуту шел обратно (т. е. вернулся на прежнее место). Тогда между мной и трамваем, двигавшимся вначале мне навстречу, за первую минуту расстояние уменьшилось на а/4, а за вторую минуту (когда этот трамвай уже догонял меня) на а/12. Итого за 2 минуты расстояние между нами уменьшилось на а/4 + а/12 = а/3.
То же было бы, если бы я стоял все время на месте, так как в итоге я все равно вернулся назад. Итак, если бы я не двигался, то за минуту (а не за две) трамвай приблизился бы ко мне на а/3 : 2 = а/6, а все расстояние а он проехал бы за 6 минут. Это означает, что мимо неподвижно стоящего наблюдателя трамваи проходят с интервалом в 6 минут.
З А Д А Ч А
Из города А в город В, расположенный ниже по течению реки, пароход шел (без остановок) 5 часов. Обратно, против течения, он шел (двигаясь с той же собственной скоростью и также не останавливаясь) 7 часов. Сколько часов идут из А в В плоты (плоты движутся со скоростью течения реки)?
Р Е Ш Е Н И Е
Обозначим через х время (в часах), нужное пароходу для того, чтобы пройти расстояние от А до В в стоячей воде (т. е. при движении с собственной скоростью), а через у — время движения плотов. Тогда за час пароход проходит 1/х расстояния АВ, а плоты (течение) 1/у этого расстояния. Поэтому вниз по реке пароход проходит за час 1/х + 1/у расстояния АВ, а вверх (против течения) 1/х - 1/у. Мы же знаем из условия задачи, что вниз по реке пароход проходит за час — расстояния, а вверх у. Получаем систему
|
{ |
1/х + 1/у = 1/5, |
| 1/х - 1/у = 1/7. |
Заметим, что для решения этой системы не следует освобождаться от знаменателей: нужно просто вычесть из первого уравнения второе. В результате мы получим:
2/у = 2/35,
откуда у = 35. Плоты идут из А в Б 35 часов.
З А Д А Ч А
Две жестянки, наполненные кофе, имеют одинаковую форму и сделаны из одинаковой жести. Первая весит 2 кг и имеет в высоту 12 см
; вторая весит 1 кг и имеет в высоту 9,5 см. Каков чистый вес кофе в жестянках?
Р Е Ш Е Н И Е
Обозначим вес содержимого большей жестянки через х, меньшей — через у. Вес самих жестянок обозначим соответственно через z и t. Имеем уравнения
|
{ |
х + z = 2. |
| y + t = 1. |
Так как веса содержимого полных жестянок относятся, как их объемы, т. е. как кубы их высот, то
x/y = 123/9,53 ≈ 2,02 или x = 2,02y.
Веса же пустых жестянок относятся, как их полные поверхности, т. е. как
квадраты их высот. Поэтому
z/t = 122/9,52
≈ 1,60 или
z = 1,60t.
Подставив
значения х и z в первое уравнение,
получаем систему
{
Решив ее,
узнаем:
y = 20/21 = 0,95, t = 0,05.
И
следовательно,
х = 1,92, z =
0,08.
2,02y + 1,60t
= 2,
y + t = 1.
Вес кофе без упаковки: в большей жестянке 1,92 кг, в меньшей — 0,94 кг.
З А Д А Ч А
На вечеринке было 20 танцующих. Мария танцевала с семью танцорами, Ольга — с восемью, Вера — с девятью и так далее до Нины, которая танцевала со всеми танцорами. Сколько танцоров (мужчин) было на вечеринке?
Р Е Ш Е Н И Е
Задача решается очень просто, если удачно выбрать неизвестное. Будем искать число не танцоров, а танцорок, которое обозначим через х:
1- я, Мария, танцевала с 6 + 1 танцорами
2- я, Ольга, » » 6 + 2 »
3- я, Вера, » » 6 + 3 »
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
х-я, Нина, » » 6 + х »
Имеем уравнение
х + (6 + х) = 20,
откуда
х = 7,
а следовательно, число танцоров —
20 - 7 = 13.
З А Д А Ч А 1
Разведчику (разведывательному кораблю), двигавшемуся в составе эскадры, дано задание обследовать район моря на 70 миль в направлении движения

Рис. 10.
эскадры. Скорость эскадры — 35 миль в час, скорость разведчика — 70 миль в час. Требуется определить, через сколько времени разведчик возвратится к эскадре.
Р Е Ш Е Н И Е
Обозначим искомое число часов через х. За это время эскадра успела пройти 35х миль, разведывательный же корабль 70х. Разведчик прошел вперед 70 миль и часть этого пути обратно, эскадра же прошла остальную часть того же пути. Вместе они прошли путь в 70x + 35x, равный 2
• 70 миль. Имеем уравнение
70x + 35x
= 110,
откуда
x = 140/105 = 11/3
часов. Разведчик возвратится к эскадре через 1 час. 20 минут.
З А Д А Ч А 2
Разведчик получил приказ произвести разведку впереди эскадры по направлению ее движения. Через 3 часа судно это должно вернуться к эскадре. Спустя сколько времени после оставления эскадры разведывательное судно должно повернуть назад, если скорость его 60 узлов, а скорость эскадры 40 узлов?
Р Е Ш Е Н И Е
Пусть разведчик должен повернуть спустя х часов; значит, он удалялся от эскадры х часов, а шел навстречу ей 3 — х часов. Пока все корабли шли в одном направлении, разведчик успел за х часов удалиться от эскадры на разность пройденных ими путей, т. е. на
60х — 40х = 20х.
При возвращении разведчика он прошел путь навстречу эскадре 60(3 - х), сама же эскадра прошла 40(3 — х). Тот и другой прошли вместе 10х. Следовательно,
60(3 - х) + 40(3 - x) = 20х,
откуда
х = 21/2.
Разведчик должен изменить курс на обратный спустя 2 часа 30 мин. после того, как он покинул эскадру.
З А Д А Ч А
По круговой дороге велодрома едут два велосипедиста с неизменными скоростями. Когда они едут в противоположных направлениях, то встречаются каждые 10 секунд; когда же едут в одном направлении, то один настигает другого каждые 170 секунд. Какова скорость каждого велосипедиста, если длина круговой дороги 170 м?
Р Е Ш Е Н И Е
Если скорость первого велосипедиста х, то в 10 секунд он проезжает 10х метров. Второй же, двигаясь ему навстречу, проезжает от встречи до встречи остальную часть круга, т. е. 170 — 10х метров. Если скорость второго у, то это составляет 10у метров; итак,
170 — 10х = 10у.
Если же велосипедисты едут один вслед другому, то в 170 секунд первый проезжает 170х метров, а второй 170у метров. Если первый едет быстрее второго, то от одной встречи до другой он проезжает на один круг больше второго, т. е.
170х — 170у = 170.
После упрощения этих уравнений получаем:
х + у = 17, х — у = 1,
откуда
х = 9, у = 8 (метров в секунду).
З А Д А Ч А
При мотоциклетных состязаниях одна из трех стартовавших одновременно машин, делавшая в час на 15 км меньше первой и на 3 км больше третьей, пришла к конечному пункту на 12 минут позже первой и на 3 минуты раньше третьей. Остановок в пути не было.
Требуется определить:
а) Как велик участок пути?
б) Как велика скорость каждой машины?
в) Какова продолжительность пробега каждой машины?
Р Е Ш Е Н И Е
Хотя требуется определить семь неизвестных величин, мы обойдемся при решении задачи только двумя: составим систему двух уравнений с двумя неизвестными.
Обозначим скорость второй машины через
х. Тогда скорость первой выразится через х + 15, а третьей — через х — 3.Длину участка пути обозначим буквой
у. Тогда продолжительность пробега обозначится:
для первой машины через . .
y : (х + 15),для второй » » . . у : х,
для третьей » » . . у : (х - 3).
Мы знаем, что вторая машина была в пути на 12 минут (т. е, на 1/5 часа) дольше первой, Поэтому
у : х - у : (х + 15) = 1/5.
Третья машина была в пути на 3 минуты (т. е. на 1/20 часа) больше второй. Следовательно,
у : (х - 3) - у : х = 1/20.
Второе из этих уравнений умножим на 4 и вычтем из первого:
у/х - у : (х + 15) - 4
[у : (х - 3) - у/х] = 0
Разделим все члены этого уравнения на
у (эта величина, как мы знаем, не равна нулю) и после этого освободимся от знаменателей. Мы получим:
(х + 15)(х - 3) - х(х - 3) - 4х(х + 15) + 4(х + 15)(х - 3) = 0,
или после раскрытия скобок и приведения подобных членов:
Зх
— 225 = 0,
откуда
х
= 75.
Зная
х, находим у из первого уравнения:
у/75 - у/90 = 1/5,
откуда
у = 90.Итак, скорости машин определены:
90, 75 и 72 километра в час.
Длина всего пути — 90
км.Разделив длину пути на скорость каждой машины, найдем продолжительность пробегов:
первой машины . . . 1 час,
второй машины . . . 1 час 12 мин.,
третьей машины . . . 1 час 15 мин.
Таким образом, все семь неизвестных определены.
З А Д А Ч А
Автомобиль проехал расстояние между двумя городами со скоростью 60 километров в час и возвратился со скоростью 40 километров в час. Какова была средняя скорость его езды?
Р Е Ш Е Н И Е
Обманчивая простота задачи вводит многих в заблуждение. Не вникнув в условия вопроса, вычисляют среднее арифметическое между 60 и 40, т. е. находят полусумму
(60 + 40) : 2 = 50.
Это «простое» решение было бы правильно, если бы поездка в одну сторону и в обратном направлении длилась одинаковое время. Но ясно, что обратная поездка (с меньшей скоростью) должна была отнять больше времени, чем езда туда. Учтя это, мы поймем, что ответ 50 — неверен.
И действительно, уравнение дает другой ответ. Составить уравнение нетрудно, если ввести вспомогательное неизвестное — именно величину
l расстояния между городами. Обозначив искомую среднюю скорость через х, составляем уравнение
2
l/x = l/a + l/b,Так как l не равно нулю, можем уравнение разделить на l ; получаем:
2/x = 1/60 + 1/40,
откуда
x = 2 : (1/60 + 1/40) = 48.
Итак, правильный ответ не 50 километров в час, а 48.
Если бы мы решали эту же задачу в буквенных обозначениях (туда автомобиль ехал со скоростью а километров в час, обратно — со скоростью b километров в час), то получили бы уравнение
2l/x = l/a + l/b,
откуда для х получаем значение
2 : (1/a + 1/b).
Эта величина называется средним гармоническим для величин а и Ь.
Итак, средняя скорость езды выражается не средним арифметическим, а средним гармоническим для скоростей движения. Для положительных а и b среднее гармоническое всегда меньше, чем их среднее арифметическое
(a + b) : 2,
что мы и видели на численном примере (48 меньше, чем 50).
Беседа об уравнениях в плане «Занимательной алгебры» не может пройти мимо решения уравнений на вычислительных машинах. Мы уже говорили о том, что вычислительные машины могут «играть» в шахматы (или шашки). Математические машины могут выполнять и другие задания, например, перевод с одного языка на другой, оркестровку музыкальной мелодии и т. д. Нужно только разработать соответствующую «программу», по которой машина будет действовать.
Конечно, мы не будем рассматривать здесь «программы» для игры в шахматы или для перевода с одного языка на другой: эти «программы» крайне сложны. Мы разберем лишь две очень простенькие «программы». Однако вначале нужно сказать несколько слов об устройстве вычислительной машины.
Выше (в гл. I) мы говорили об устройствах, которые позволяют производить многие тысячи вычислений в секунду. Эта часть вычислительной машины, служащая для непосредственного выполнения действий, называется арифметическим устройством. Кроме того, машина содержит управляющее устройство (регулирующее работу всей машины) и так называемую память. Память, или, иначе, запоминающее устройство, представляет собой хранилище для чисел и условных сигналов. Наконец, машина снабжена особыми устройствами для ввода новых цифровых данных и для выдачи готовых результатов. Эти готовые результаты машина печатает (уже в десятичной системе) на специальных карточках.
Всем хорошо известно, что звук можно записать на пластинку или на пленку и затем воспроизвести. Но запись звука на пластинку может быть произведена лишь один раз: для новой записи нужна уже новая пластинка. Несколько иначе осуществляется запись звука в магнитофоне: при помощи намагничивания особой ленты. Записанный звук можно воспроизвести нужное число раз, а если запись оказалась уже ненужной, ее можно «стереть» и произвести на той же ленте новую запись. На одной и той же ленте можно произвести одну за другой несколько записей, причем при каждой новой записи предыдущая «стирается».
На подобном же принципе основано действие запоминающих устройств. Числа и условные сигналы записываются (при помощи электрических, магнитных или механических сигналов) , на специальном барабане, ленте или другом устройстве. В нужный момент записанное число может быть «прочтено», а если оно уже больше не нужно, то его молено стереть, а на его месте записать другое число. «Запоминание» и «чтение» числа или условного сигнала длятся всего лишь миллионные доли секунды.
«Память» может содержать несколько тысяч ячеек, каждая ячейка — несколько десятков элементов, например магнитных. Для записи чисел по двоичной системе счисления условимся считать, что каждый намагниченный элемент изображает цифру 1, а ненамагниченный — цифру 0. Пусть, например, каждая ячейка памяти содержит 25 элементов (или, как говорят, 25 «двоичных разрядов», причем первый элемент ячейки служит для обозначения знака числа (+ или —), следующие 14 разрядов служат для записи целой части числа, а последние 10 разрядов — для записи дробной части. На рис. 11 схематически изображены две ячейки памяти; в каждой по 25 разрядов. Намагниченные элементы обозначены знаком +, ненамагниченные обозначены знаком —. Рассмотрим верхнюю из изображенных ячеек (запятая показывает, где начинается дробная часть числа, а пунктирная линия отделяет первый разряд, служащий для записи знака, от остальных).
В ней записано (в двоичной системе счисления) число +1011,01 или — в привычной для нас десятичной системе счисления — число 11,25.Кроме чисел в ячейках памяти записываются приказы, из которых состоит программа. Рассмотрим, как выглядят приказы для так называемой трехадресной машины. В этом случае при записи приказа ячейка памяти разбивается на 4 части (пунктирные линии на нижней ячейке, рис. 11). Первая часть служит для обозначения операции, причем операции записываются числами (номерами).
Например,
сложение — операция 1,
вычитание — операция 2,
умножение — операция 3 и т. д.
Приказы расшифровываются так: первая часть ячейки — номер операции, вторая и третья части — номера ячеек (а д р е с а), из которых надо взять числа для выполнения, этой операции, четвертая часть — номер ячейки (адрес), куда следует отправить полученный результат. Например, на рис. 11 (нижняя
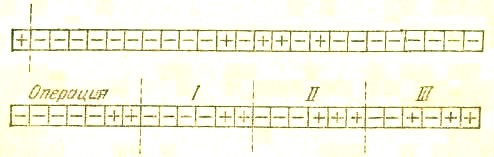
Рис. 11.
строка) записаны в двоичной системе числа 11, 11, 111, 1011 или в десятичной системе: 3, 3, 7, 11, что означает следующий приказ: выполнить операцию 3 (т. е. умножение) над числами, находящимися в третьей и седьмой ячейках памяти, а полученный результат «запомнить» (т. е. записать) в одиннадцатой ячейке.
В дальнейшем мы будем записывать числа и приказы не условными значками, как на рис. 11, а прямо в десятичной системе счисления. Например, приказ, изображенный в нижней строке рис. 11, запишется так:
умножение 3 7 11
Рассмотрим теперь два простеньких примера программ.
Программа 1
1) сложение 4 5 4
2) умножение 4 4 →
3) п. у. 1
4) 0
5) 1
Посмотрим, как будет работать машина, у которой в первых пяти ячейках записаны эти данные.
1-й приказ: сложить числа, записанные в 4-й и 5-й ячейках, и отправить результат снова в 4-ю ячейку (вместо того, что там было записано ранее). Таким образом, машина запишет в 4-ю ячейку число 0+1 = — 1. После выполнения 1-го приказа в 4-й и 5-й ячейках будут следующие числа:
4) 1,
5) 1.
2-й приказ: умножить число, имеющееся в 4-й ячейке, на себя (т. е. возвести его в квадрат) и результат, т. е. 12, выписать на карточку (стрелка означает выдачу готового результата).
3-й приказ: передача управления в 1-ю ячейку. Иначе говоря, приказ п. у. означает, что надо снова по порядку выполнять все приказы, начиная с 1-го. Итак, снова 1-й приказ.
1-й приказ: сложить числа, имеющиеся в 4-й и 5-й ячейках, и результат снова записать в 4-й ячейке. В результате в 4-й ячейке будет число 1 + 1 = 2:
4) 2,
5) 1.
2-й приказ: возвысить в квадрат число, стоящее в 4-й ячейке, и полученный результат, т. е. 22, выписать на карточку (стрелка — выдача результата).
3-й приказ: передача управления в первую ячейку (т. е. опять переход к 1-му приказу).
1-й приказ: число 2 + 1 = 3 отправить в 4-ю ячейку:
4) 3,
5) 1.
2-й приказ: выписать на карточку число З2.
3-й приказ: передача управления в 1-ю ячейку и т. д.
Мы видим, что машина вычисляет один за другим квадраты целых чисел и выписывает их на карточку. Заметьте, что каждый раз набирать новое число вручную не надо: машина сама перебирает подряд целые числа и возводит их в квадрат. Действуя по этой программе, машина вычислит квадраты всех целых чисел, скажем, от 1 до 10000 в течение нескольких секунд (или даже долей секунды).
Следует отметить, что в действительности программа для вычисления квадратов целых чисел должна быть несколько сложнее той, которая приведена выше. Это прежде всего относится ко 2-му приказу. Дело в том, что выписывание готового результата на карточку требует во много раз больше времени, чем выполнение машиной одной операции. Поэтому готовые результаты сначала «запоминаются» в свободных ячейках «памяти», а уже после этого («не спеша») выписываются на карточку. Таким образом, первый окончательный результат должен «запоминаться» в 1-й свободной ячейке «памяти», второй результат — во 2-й свободной ячейке, третий —- в 3-й и т. д. В приведенной выше упрощенной программе это никак не было учтено.
Кроме того, машина не может долго заниматься вычислением квадратов — не хватит ячеек «памяти», — а «угадать», когда машина уже вычислила нужное нам число квадратов, чтобы в этот момент выключить ее, — невозможно (ведь машина производит многие тысячи операций в секунду!). Поэтому предусмотрены особые приказы для остановки машины в нужный момент. Например, программа может быть составлена таким образом, что машина вычислит квадраты всех целых чисел от 1 до 10000 и после этого автоматически выключится.
Если и другие более сложные виды приказов, на которых мы здесь для простоты не останавливаемся.
Вот как выглядит в действительности программа для вычисления квадратов всех целых чисел от 1 до 10 000:
Программа 1а
1) сложение 8 9 8
2) умножение 8 8 10
3) сложение 2 6 2
4) у. п. у. 8 7 1
5) стоп
6) 0 0 1
7) 10000
8) 0
9) 1
10) 0
11) 0
12) 0
. . .
Первые два приказа мало отличаются от тех, которые были в предыдущей упрощенной программе. После выполнения этих двух приказов в 8-й, 9-й и 10-й ячейках будут следующие числа:
8) 1
9) 1
10) 12
Третий приказ очень интересен: надо сложить то, что стоит во 2-й и 6-й ячейках, и результаты снова записать во 2-й ячейке, после чего 2-я ячейка будет иметь вид
2) умножение 8 8 11.
Как видите, после выполнения третьего приказа меняется второй приказ, вернее меняется один из адресов 2-го приказа. Ниже мы выясним, для чего это делается.
Четвертый приказ: условная передача управления (вместо 3-го приказа в рассмотренной ранее программе). Этот приказ выполняется так: если число, стоящее в 8-й ячейке, меньше числа, стоящего в 7-й ячейке, то передается управление в 1-ю ячейку; в противном случае выполняется следующий (т. е. 5-й) приказ. В нашем случае действительно 1 < 10000, так что происходит передача управления в 1-ю ячейку. Итак, снова 1-й приказ.
После выполнения 1-го приказа в 8-й ячейке будет число 2.
Второй приказ, который теперь имеет вид
2) умножение 8 8 11,
заключается в том, что число 22 направляется в 11-ю ячейку. Теперь ясно, зачем был выполнен ранее 3-й приказ: новое число, т. е. 22, должно попасть не в 10-ю ячейку, которая уже занята, а в следующую.
После выполнения 1-го и, 2-го приказов у нас будут следующие числа:
8) 2
9) 1
10) 12
11) 22
После выполнения 3-го приказа 2-я ячейка примет вид
2) умножение 8 8 12,
т. е. машина «подготовилась» к тому, чтобы записать новый результат в следующую, 12-ю ячейку. Так как в 8-й ячейке все еще стоит меньшее число, чем в 9-й ячейке, то 4-й приказ означает снова передачу управления в 1-ю ячейку.
Теперь после выполнения 1-го и 2-го приказов получим:
8) 3
9) 1
10) 12
11) 22
12) З2
До каких пор машина будет по этой программе вычислять квадраты? До тех пор, пока в 8-й ячейке не появится число 10000, т. е. пока не будут вычислены квадраты чисел от 1 до 10000. После этого 4-й приказ уже не передаст управления в 1-ю ячейку (так как в 8-й ячейке будет стоять число, не меньшее, а равное числу, стоящему в 7-й ячейке), т. е. после 4-го приказа машина выполнит 5-й приказ: остановится (выключится).
Рассмотрим теперь более сложный пример программы: решение систем уравнений. При этом мы рассмотрим упрощенную программу, При Шёл а ни и читатель сам подумает о том, как должка выглядеть такая программа в полном виде.
Пусть задана система уравнений
| { | ах + ву = с |
| dx + ey = f |
Эту систему нетрудно решить:
x = (ce - bf) : (ae - bd), y = (af - cd) : (ae - bd).
Для решения такой системы (с заданными числовыми значениями
коэффициентов
Рассмотрим соответствующую программу. Будем считать, что даны сразу несколько систем
:
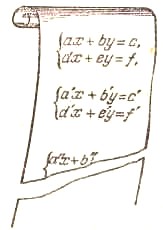
с числовыми значениями коэффициентов
a, b, с, d, e, f, a', b', ...Вот соответствующая программа:
Программа 2

1-й приказ: составить произведение чисел, стоящих в 28-й и 30-й ячейках, и направить результат в 20-ю ячейку. Иначе говоря, в 20-й ячейке будет записано число се
.Аналогично выполняются приказы 2-й — 6-й. После их выполнения в ячейках 20-й — 25-й будут находиться следующие числа:
20)
се21)
bf22)
ае23) bd
24)
af25) cd
7-й приказ: из числа, стоящего в 20-й ячейке, вычесть число, стоящее в 21-й ячейке, и результат (т. е. се — bf) снова записать в 20-ю ячейку.
Аналогично выполняются приказы 8-й и 9-й. В результате в ячейках 20-й, 21-й, 22-й окажутся следующие числа:
20)
се — bf21)
ае — bd22)
af — сd
10-й и 11-й приказы: составляются частные
(ce - bf) : (ae - bd) и (af - cd) : (ae - bd)
и выписываются на карточку (т. е. выдаются как готовые результаты). Это и есть значения неизвестных, получаемых из первой системы уравнений.
Итак, первая система решена. Зачем же дальнейшие приказы? Дальнейшая часть программы (ячейки 12-я
- 19-я) предназначена для того, чтобы заставить машину «подготовиться» к решению второй системы уравнений. Посмотрим, как это происходит. Приказы с 10-го по 17-й заключаются в том, что к содержимому ячеек 1-й - 6-й прибавляется запись, имеющаяся в 19-й ячейке, а результаты снова остаются в ячейках 1-й - 6-й. Таким образом, после выполнения 17-го приказа первые шесть ячеек будут иметь следующий вид:
1)
X 34 36 202) X 33
37 213) X 32
35 224) X 33
35 235) X 32
37 246) X 34
35 25
18-й приказ: передача
управления в первую ячейку
Чем же отличаются новые записи в первых шести ячейках от прежних записей? Тем, что первые два адреса в этих ячейках имеют номера не от 26 до 31, как прежде, а номера от 32 до 37. Иначе говоря, машина снова будет производить те же действия, но числа будет брать не из ячеек 26-й - 31-й, а из ячеек 32-й - 37-й, где стоят коэффициенты второй системы уравнений. В результате машина решит вторую систему уравнений. После решения второй системы машина перейдет к третьей и т. д.
Из сказанного становится ясным, как важно уметь составить правильную «программу». Ведь машина «сама» ничего делать не «умеет». Она может лишь выполнять заданную ей программу. Имеются программы для вычисления корней, логарифмов, синусов, для решения уравнений высших степеней и т. д. Мы уже говорили выше о том, что существуют программы для игры в шахматы, для перевода с иностранного языка, .
.. Конечно, чем сложнее задание, тем сложнее соответствующая программа.Заметим в заключение, что существуют так называемые программирующие программы, т. е. такие, с помощью которых сама машина может составить требуемую для решения задачи программу. Это значительно облегчает составление программы, которое часто бывает очень трудоемким.