Мой сайт

Диофантовы уравнения

Разберем особый вид уравнений, называемые диофантовыми.

Диофантовыми уравнениями называют алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях должно быть не менее двух (если не ограничиваться только целыми числами). Диофантовы уравнения имеют, как правило, много решений, поэтому их называют неопределенными уравнениями.

К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величин могут быть только целыми числами.

Современной постановкой диофантовых задач мы обязаны Ферма.

Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Надо сказать, что это не было изобретением Ферма - он только возродил интерес к поиску целочисленных решений. А вообще задачи, допускающие только целые решения, были распространены во многих странах в очень далёкие от нас времена.

Существует множество решений Диофантовых уравнений: Способ перебора вариантов, Алгоритм Евклида, Малая теорема Ферма и остальные не менее известные способы.

Решение уравнений в целых числах является одной из древнейших математических задач. Уже в начале 2-го тысячелетия до н. э. вавилоняне умели решать системы таких уравнений с двумя неизвестными. Наибольшего расцвета эта область математики достигла в Древней Греции. Основным источником для нас является "Арифметика" Диофанта (вероятно, 3 в. н. э.), содержащая различные типы уравнений и систем. В ней Диофант (по его имени - "Д. у.") предвосхищает ряд методов исследования уравнений 2-й и 3-й степеней, развившихся только в 19 в.

Создание древнегреческими учеными теории рациональных чисел привело к рассмотрению рациональных решений неопределенных уравнений. Эта точка зрения последовательно проводится в книге Диофанта. Хотя сочинение Диофанта содержит лишь решения конкретных Д. у., однако есть основания считать, что он владел некоторыми общими приемами.

Покупка свитера

З А Д А Ч А

Вы должны уплатить за купленный в магазине свитер 19 руб. У вас одни лишь трехрублевки, у кассира — только пятирублевки. Можете ли вы при наличии таких денег расплатиться с кассиром и как именно?

Вопрос задачи сводится к тому, чтобы узнать, сколько должны вы дать кассиру трехрублевок, чтобы, получив сдачу пятирублевками, уплатить 19 рублей. Неизвестных в задаче два — число (х) трехрублевок и число (у) пятирублевок. Но можно составить только одно уравнение:

Зх — 5у = 19.

Хотя одно уравнение с двумя неизвестными имеет бесчисленное множество решений, но отнюдь еще не очевидно, что среди них найдется хоть одно с целыми положительными х и у (вспомним, что это — числа кредитных билетов). Вот почему алгебра разработала метод решения подобных «неопределенных» уравнений. Заслуга введения их в алгебру принадлежит первому европейскому представителю этой науки, знаменитому математику древности Диофанту, отчего такие уравнения часто называют «диофантовыми».

Р Е Ш Е Н И Е

На приведенном примере покажем, как следует решать подобные уравнения.

Надо найти значения х и у в уравнении

Зх — 5у= 19,

зная при этом, что х и у — числа целые и положительные.

Уединим то неизвестное, коэффициент которого меньше, т. е. член Зх; получим:

Зх = 19 + 5у,

откуда

x = (19 + 5у) : 3 = 6 + y + (1 + 2у) : 3.

Так как х, 6 и у — числа целые, то равенство может быть верно лишь при условии, что (1 + 2у) : 3 есть также целое число. Обозначим его буквой t. Тогда

х = 6 + у + t,

где

t = (1 + 2y) : 3,

и, значит,

3t = 1 + 2y, 2y = 3t — 1.

Из последнего уравнения определяем у:

y = (3t - 1) : 2 = t + (t - 1) : 2.

Так как у и t — числа целые, то и (t - 1) : 2 должно быть некоторым целым числом t₁. Следовательно,

у = t + t₁,

причем

t₁ = (t - 1) : 2,

откуда

2t₁ = t - 1 и t = 2t₁ + 1.

Значение t = 2t₁ + 1 подставляем в предыдущие равенства:

y = t + t₁ = (2t₁ + 1) + t₁ = 3t₁ + 1,

y = 6 + y + t = 6 + (3t₁ + 1) + (2t₁ + 1) = 8 + 5t₁.

Итак, для x и у мы нашли выражения

х = 8 + 5t₁,

У = 1 + 3t₁.

Числа х и у, мы знаем, — не только целые, но и положительные, т. е. большие чем 0. Следовательно,

8 + 5t₁ > 0,

1 + 3t₁ > 0.

Из этих неравенств находим:

5t₁ > — 8 и t₁ > — 8/5,

Зt₁ > — 1 и t₁ > — 1/3.

Этим величина t₁ ограничивается; она больше чем — 1/3 (и, значит, подавно больше чем — 8/5). Но так как t₁ — число целое, то заключаем, что для него возможны лишь следующие значения:

t₁ = 0, 1, 2, 3, 4, ...

Соответствующие значения для х и у таковы:

x = 8 + 5t₁ = 8, 13, 18, 23, ...,

y = 1 + 3t₁ = 1, 4, 7, 10, ...

Теперь мы установили, как может быть произведена уплата:

вы либо платите 8 трехрублевок, получая одну пятирублевку сдачи:

8 • 3 — 5 = 19,

либо платите 13 трехрублевок, получая сдачи 4 пятирублевки:

13 • 3 — 4 • 5 = 19

и т. д.

Теоретически задача имеет бесчисленный ряд решений, практически же число решений ограничено, так как ни у покупателя, ни у кассира нет бесчисленного множества кредитных билетов. Если, например, у каждого всего по 10 билетов, то расплата может быть произведена только одним способом: выдачей 8 трехрублевок и получением 5 рублей сдачи. Как видим, неопределенные уравнения практически могут давать вполне определенные пары решений.

Возвращаясь к нашей задаче, предлагаем читателю в качестве упражнения самостоятельно решить ее вариант, а именно рассмотреть случай, когда у покупателя только пятирублевки, а у кассира только трехрублевки. В результате получится такой ряд решений:

х = 5, 8, 11, ...,

y = 2, 7, 12, ...

Действительно,

5 • 5 - 2 • 3 = 19,

8 • 5 - 7 • 3 = 19,

11 • 5 - 12 • 3 = 19,

. . . . . . . . . . . . . . .

Мы могли бы получить эти результаты также и из готового уже решения основной задачи, воспользовавшись простым алгебраическим приемом. Так как давать пятирублевки и получать трехрублевки все равно, что «получать отрицательные пятирублевки» и «давать отрицательные трехрублевки», то новый вариант задачи решается тем же уравнением, которое мы составили для основной задачи:

Зх — 5у = 19,

но при условии, что х и у — числа отрицательные. Поэтому из равенств

х = 8 + 5t₁, у = 1 + 3t₁

мы, зная, что х < 0 и у < 0, выводим:

8 + 5t₁ < 0, 1 + 3t₁ < 0

и, следовательно,

t₁ < - 8/5.

Принимая t₁ = — 2, — 3, — 4 и т. д., получаем из предыдущих формул следующие значения для х и у:

t₁ = - 2, - 3, - 4,

x = - 2, - 7, - 12,

y = - 5, - 8, - 11.

Первая пара решений, x = - 2, у = - 5, означает, что покупатель «платит минус 2 трехрублевки» и «получает минус 5 пятирублевок», т. е. в переводе на обычный язык — платит 5 пятирублевок и получает сдачи 2 трехрублевки. Подобным же образом истолковываем и прочие решения.

Ревизия магазина

З А Д А Ч А

При ревизии торговых книг магазина одна из записей оказалась залитой чернилами и имела такой вид:

Невозможно было разобрать число проданных метров, но было несомненно, что число это не дробное; в вырученной сумме можно было различить только последние три цифры, да установить еще, что перед ними были три какие-то другие цифры.

Может ли ревизионная комиссия по этим следам установить запись?

Р Е Ш Е Н И Е

Обозначим число метров через х. Вырученная сумма выразится в копейках через

4936x.

Число, выражаемое тремя залитыми цифрами в записи денежной суммы, обозначим через у. Это, очевидно, число тысяч копеек, а вся сумма в копейках изобразится так:

1000y + 728.

Имеем уравнение

4936x = 1000y + 728,

или, после сокращения на 8,

617x — 125y = 91.

В этом уравнении х и у — числа целые и притом у не больше 999, так как более чем из трех цифр оно состоять не может. Решаем уравнение, как раньше было указано:

125y = 617x — 91,

y = 5x — 1 + (34 - 8x) : 125 = 5x - 1 + [2(17 - 4x) : 125] = 5x - 1 + 2t.

(Здесь мы приняли 617/125 = 5 - 8/125, так как нам выгодно иметь возможно меньшие остатки. Дробь

2(17 — 4х)

125

есть целое число, а так как 2 не делится на 125, то (17 - 4х) : 125, должно быть целым числом, которое мы и обозначили через t.)

Далее из уравнения

(17 — 4х) : 125 = t

имеем:

17 — 4х = 125t,

х = 4 — 31t + (1 - t) : 4 = 4 — 31t + t₁,

где

t₁ = (1 - t) : 4,

и, следовательно,

4t₁ = 1 - t;

t = 1 - 4t₁;

x = 125t₁ - 27,

у = 617t₁ - 134.

Мы знаем, что

100 ≤ y < 1000.

Следовательно,

100 ≤ 617t₁ — 134 < 1000,

откуда

t₁ ≥ 234/617 и t₁ < 1134/617.

Очевидно, для t₁ существует только одно целое значение:

t₁ = 1,

и тогда

х = 98, у = 483,

т. е. было отпущено 98 метров на сумму 4837 р. 28 к. Запись восстановлена.

Покупка почтовых марок

З А Д А Ч А

Требуется на один рубль купить 40 штук почтовых марок — копеечных, 4-копеечных и 12-копеечных. Сколько окажется марок каждого достоинства?

Р Е Ш Е Н И Е

В этом случае у нас имеется два уравнения с тремя неизвестными:

х + 4у + 12z = 100,

х + у + z = 40,

где х — число копеечных марок, у — 4-копеечных, z — 12-копеечных.

Вычитая из первого уравнения второе, получим одно уравнение с двумя неизвестными:

3у + 11z = 60.

Находим у:

y = 20 - 11 • z/3.

Очевидно, z/3 — число целое. Обозначим его через t.

Имеем:

у = 20 — 11t,

z = 3t.

Подставляем выражения для у и z во второе из исходных уравнений:

x + 20 — 11t + 3t = 40;

получаем:

x = 20 + 8t.

Так как x ≥ 0, у ≥ 0 и z ≥ 0, то нетрудно установить границы для t:

0 ≤ t ≤ 1⁹/₁₁,

откуда заключаем, что для t возможны только два целых значения:

t = 0 и t = 1.

Соответствующие значения х, у и z таковы:

t =	0	1
х =	20	28
У =	20	9
z =	0	3

Проверка

20 • 1 + 20 • 4 + 0 • 12 = 100,

28 • 1 + 9 • 4 + 3 • 12 = 100.

Итак, покупка марок может быть произведена только двумя способами (а если потребовать, чтобы была куплена хотя бы одна марка каждого достоинства, — то только одним способом).

Следующая задача — в том же роде.

Покупка фруктов

З А Д А Ч А

На 5 руб. куплено 100 штук разных фруктов. Цены на фрукты таковы:

арбуз, штука ....... 50 коп.

яблоки, » ........... 10 »

сливы, » ............ 1 »

Сколько фруктов каждого рода было куплено?

Р Е Ш Е Н И Е

Обозначив число арбузов через х, яблок через у и слив через z, составляем два уравнения:

{	50x + 10y + 1z = 500,
	x + y + z = 100.

Вычтя из первого уравнения второе, получим одно уравнение с двумя неизвестными:

49x + 9y = 400.

Дальнейший ход решения таков:

y = (400 - 49x) : 9 = 44 - 5x + [4(1 - x)] : 9 = 44 - 5x + 4t,

t = (1 - x) : 9, x = 1 - 9t,

y = 44 - 5(1 - 9t) + 4t = 39 + 49t.

Из неравенств

1 - 9t ≥ 0 и 39 + 49t ≥ 0

устанавливаем, что

1/9 ≥ t ≥ - 39/49

и, следовательно, t = 0. Поэтому

x = 1, у = 39.

Подставив эти значения x и у во второе уравнение, получаем: z = 60.

Рис. 12.

Итак, куплены были 1 арбуз, 39 яблок и 60 слив. Других комбинаций быть не может.

Отгадать день рождения

З А Д А Ч А

Уменье решать неопределенные уравнения дает возможность выполнить следующий математический фокус.

Вы предлагаете товарищу умножить число даты его рождения на 12, а номер месяца — на 31. Он сообщает вам сумму обоих произведений, и вы вычисляете по ней дату рождения.

Если, например, товарищ ваш родился 9 февраля, то он выполняет следующие выкладки:

9 • 12 = 108, 2 • 31 = 62,

108 + 62 = 170.

Это последнее число, 170, он сообщает сам, и вы определяете задуманную дату. Как?

Р Е Ш Е Н И Е

Задача сводится к решению неопределенного уравнения

12х + 31y = 170

в целых и положительных числах, причем число месяца х не больше 31, а номер месяца у не больше 12.

x = (170 - 31y) : 12 = 14 - 3y + (2 + 5y) : 12 = 14 - 3y + t,

2 + 5y = 12t,

y = (-2 + 12t) : 5 = 2t - 2 • (1 - t) : 5 = 2t - 2t₁,

1 - t = 5t₁, t = 1 - 5t₁,

y = 2(1 - 5t₁) - 2t₁ = 2 - 12t₁,

x = 14 - 3(2 - 12t₁) + 1 - 5t₁ = 9 + 31t₁.

Зная, что 31 ≥ х > 0 и 12 ≥ у > 0, находим границы для t₁:

- ⁹/₃₁ < t₁ < ¹/₆.

Следовательно,

t₁ = 0, х = 9, у = 2.

Дата рождения 9-е число второго месяца, т. е, 9 февраля.

Можно предложить и другое решение, не использующее уравнений. Нам сообщено число а — 12х + 31у. Так как 12х + 24у делится на 12, то числа 7у и а имеют одинаковые остатки от деления на 12. Умножив на 7, найдем, что 49у и 7а имеют одинаковые остатки от деления на 12. Но 49у = 48у + у, а 48у делится на 12, Значит, у и 7а имеют одинаковые остатки от деления на 12. Иными словами, если а не делится на 12, то у равен остатку от деления числа 7а на 12; если же а делится на 12, то у = 12. Этим число у (номер месяца) вполне определяется. Ну, а зная у, уже ничего не стоит узнать х.

Маленький совет: прежде чем узнавать остаток от деления числа 7а на 12, замените само число а его остатком от деления на 12 — считать будет проще. Например, если а = 170, то вы должны произвести в уме следующие вычисления:

170 = 12 • 14 + 2 (остаток, значит, равен 2);

2 • 7 = 14; 14 = 12 • 1 + 2 (значит, у = 2);

x = (170 - 31y) : 12 = (170 - 31 • 2) : 12 = 108 : 12 = 9 (значит, x = 9),

Теперь вы можете сообщить товарищу дату его рождения: 9 февраля.

Докажем, что фокус всегда удается без отказа, т. e. что уравнение всегда имеет только одно решение в целых положительных числах. Обозначим число, которое сообщил ваш товарищ, через а, так что нахождение даты его рождения сводится к решению уравнения

12х + 31y = а.

Станем рассуждать «от противного». Предположим, что это уравнение имеет два различных решения в целых положительных числах, а именно решение x₁, у₁ и решение х₂, y₂, причем х₁ и х₂ не превосходят 31, а y₁ и у₂ не превосходят 12. Мы имеем:

12x₁ + 31y₁ = а,

12x₂ + 31y₂ = а.

Вычитая из первого равенства второе, получим:

12(х₁ — х₂) + 31(y₁ — у₂) = 0.

Из этого равенства вытекает, что число 12(x₁ — х₂) делится на 31. Так как х₁ и х₂ — положительные числа, не превосходящие 31, то их разность х₁ — х₂ по величине меньше чем 31. Поэтому число 12(x₁ — х₂) может делиться на 31 только в том случае, когда x₁ = x₂, т. е, когда первое решение совпадает со вторым. Таким образом, предположение о существовании двух различных решений приводит к противоречию.

Продажа кур

С Т А Р И Н Н А Я З А Д А Ч А

Три сестры пришли на рынок с курами. Одна принесла для продажи 10 кур, другая 16, третья 26. До полудня они продали часть своих кур по одной и той же цене. После полудня, опасаясь, что не все куры будут проданы, они понизили цену и распродали оставшихся кур снова по одинаковой цене. Домой все трое вернулись с одинаковой выручкой: каждая сестра получила от продажи 35 рублей.

По какой цене продавали они кур до и после полудня?

Р Е Ш Е Н И Е

Обозначим число кур, проданных каждой сестрой до полудня, через х, у, z. Во вторую половину дня они продали 10 — х, 16 — у, 26 — z кур. Цену до полудня обозначим через m, после полудня — через n. Для ясности сопоставим эти обозначения:

Число проданных кур				Цена
До полудня	x	y	z	m
После полудня	10 - х	16 - у	26 - z	n

Первая сестра выручила:

mх + n(10 — х); следовательно, mx + n(10 — x) = 35;

вторая:

my + n(16 — у); следовательно, my + n(16 — у) = 35;

третья:

mz + n(26 — z); следовательно, mz + n(26 — z) = 35.

Преобразуем эти три уравнения:

{	(m - n)x + 10n = 35,
	(m - n)y + 16n = 35,
	(m - n)z + 26n = 35.

Вычтя из третьего уравнения первое, затем второе, получим последовательно:

{	(m - n)(z - x) + 16n = 0,
	(m - n)(z - y) + 10n =0.

или

{	(m - n)(x - z) = 16n,
	(m - n)(y - z) = 10n.

Делим первое из этих уравнений на второе:

(x - z) : (y - z) = ⁸/₅, или (x - z) : 8 = (y - z) : 5.

Так как х, у, z — числа целые, то и разности х — z, у — z — тоже целые числа. Поэтому для существования равенства

(x - z) : 8 = (y - z) : 5

необходимо, чтобы х — z делилось на 8, а у — z на 5, Следовательно,

(x - z) : 8 = t = (y - z) : 5,

откуда

x = z + 8t,

у = z + 5t.

Заметим, что число t — не только целое, но и положительное, так как х > z (в противном случае первая сестра не могла бы выручить столько же, сколько третья).

Так как х < 10, то

z + 8t < 10.

При целых и положительных z и t последнее неравенство удовлетворяется только в одном случае: когда z = 1 и t = 1. Подставив эти значения в уравнения

x = z + 8t и у = z + 5t,

находим: х = 9, у = 6.

Теперь, обращаясь к уравнениям

mx + n(10 — х) = 35,

my + n(16 — у) = 35,

mz + n(26 — z) = 35

и подставив в них найденные значения х, у, z, узнаем цены, по каким продавались куры:

m = 3³/₄ руб., n = 1¹/₄ руб.

Итак, куры продавались до полудня по 3 руб. 75 коп., после полудня по 1 руб. 25 коп.

Два числа и четыре действия

З А Д А Ч А

Предыдущую задачу, которая привела к трем уравнениям с пятью неизвестными, мы решили не по общему образцу, а по свободному математическому соображению. Точно так же будем решать и следующие задачи, приводящие к неопределенным уравнениям второй степени.

Вот первая из них.

Над двумя целыми положительными числами были выполнены следующие четыре действия:

1) их сложили;

2) вычли из большего меньшее;

3) перемножили;

4) разделили большее на меньшее.

Полученные результаты сложили — составилось

243. Найти эти числа.

Р Е Ш Е Н И Е

Если большее число х, меньшее у, то

(х + y) + (х - xy) + xy +^x/_y = 243.

Если это уравнение умножить на у, затем раскрыть скобки и привести подобные члены, то получим:

х(2у + у²+ 1) = 243у.

Но 2у+ у² + 1 = (у + 1)². Поэтому

x = 243y : (y + 1)².

Чтобы х было целым числом, знаменатель (у + 1)²должен быть одним из делителей числа 243 (потому что у не может иметь общие множители с y + 1). Зная, что 243 = З⁵, заключаем, что 243 делится только на следующие числа, являющиеся точными квадратами: 1, З², 9². Итак, (у + I)² должно быть равно 1, З² или 9², откуда (вспоминая, что у должно быть положительным) находим, что у равно 8 или 2.

Тогда х равно

243 • 8 : 81 или 243 • 2 : 9.

Итак, искомые числа: 24 и 8 или 54 и 2.

Какой прямоугольник?

З А Д А Ч А

Стороны прямоугольника выражаются целыми числами. Какой длины должны они быть, чтобы периметр прямоугольника численно равнялся его площади?

Р Е Ш Е Н И Е

Обозначив стороны прямоугольника через х и у, составляем уравнение

2х + 2у = ху,

откуда

x = 2y : (y - 2).

Так как х и у должны быть положительными, то положительным должно быть и число у — 2, т. е. у должно быть больше 2,

Заметим теперь, что

x = 2y : (y - 2) = [2(y - 2) + 4] : (y - 2) = 2 + 4 : (y - 2).

Так как x должно быть целым числом, то выражение 4 : (y - 2) должно быть целым числом. Но при у > 2 это возможно лишь, если у равно 3, 4 или б. Соответствующие значения х будут 6, 4, 3.

Итак, искомая фигура есть либо прямоугольник со сторонами 3 и 6, либо квадрат со стороной 4.

Два двузначных числа

З А Д А Ч А

Числа 46 и 96 обладают любопытной особенностью: их произведение не меняет своей величины, если переставить их цифры.

Действительно,

46 • 96 = 4416 = 64 • 69.

Требуется установить, существуют ли еще другие пары двузначных чисел с тем же свойством. Как разыскать их все?

Р Е Ш Е Н И Е

Обозначив цифры искомых чисел через х и у, z и t, составляем уравнение

(10x + у) (10z + t) = (10y + х) (10t + z).

Раскрыв скобки, получаем после упрощений:

xz = yt,

где х, у, z, t — целые числа, меньшие 10. Для разыскания решений составляем из 9 цифр все пары с разными произведениями:

1 • 4 = 2 • 2 2 • 8 = 4 • 4

1 • 6 = 2 • 3 2 • 9 = 3 • 6

1 • 8 = 2 • 4 3 • 8 = 4 • 6

1 • 9 = 3 • 3 4 • 9 = 6 • 6

2 • 6 = 3 • 4

Всех равенств 9. Из каждого можно составить одну или две искомые группы чисел. Например, из равенства 1 • 4 = 2 • 2 составляем одно решение:

12 • 42 = 21 • 24

Из равенства 1 • 6 = 2 • 3 находим два решения:

12 • 63 = 21 • 36, 13 • 62 = 31 • 26.

Таким образом разыскиваем следующие 14 решений:

12 • 42 = 21 • 24 23 • 96 = 32 • 69

12 • 63 = 21 • 36 24 • 63 = 42 • 36

12 • 84 = 21 • 48 24 • 84 = 42 • 48

13 • 62 = 31 • 26 26 • 93 = 62 • 39

13 • 93 = 31 • 39 34 • 86 = 43 • 68

14 • 82 = 41 • 28 36 • 84 = 63 • 48

23 • 64 = 32 • 46 46 • 96 = 64 • 69

Пифагоровы числа

Удобный и очень точный способ, употребляемый землемерами для проведения на местности перпендикулярных линий, состоит в следующем. Пусть через точку А требуется к прямой MN провести перпендикуляр (рис. 13). Откладывают от А по направлению AM три раза какое-нибудь расстояние а. Затем завязывают на шнуре три узла, расстояния между которыми равны 4а и 5а.

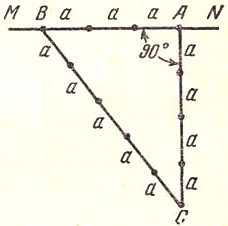
Рис. 13.

Приложив крайние узлы к точкам A и В, натягивают шнур за средний узел. Шнур расположится треугольником, в котором угол А — прямой.

Этот древний способ, по-видимому, применявшийся еще тысячелетия назад строителями египетских пирамид, основан на том, что каждый треугольник, стороны которого относятся, как 3 : 4 : 5, согласно общеизвестной теореме Пифагора, — прямоугольный, так как

3² + 4² = 5².

Кроме чисел 3, 4, 5, существует, как известно, бесчисленное множество целых положительных чисел а, b, с, удовлетворяющих соотношению

а² + b² - с².

Они называются пифагоровыми числами. Согласно теореме Пифагора такие числа могут служить длинами сторон некоторого прямоугольного треугольника; поэтому а и b называют «катетами», а с — «гипотенузой».

Ясно, что если а, b, с есть тройка пифагоровых чисел, то и pa, pb, рс, где р —-целочисленный множитель, — пифагоровы числа. Обратно, если пифагоровы числа имеют общий множитель, то на этот общий множитель молено их все сократить, и снова получится тройка пифагоровых чисел. Поэтому будем вначале исследовать лишь тройки взаимно простых пифагоровых чисел (остальные получаются из них умножением на целочисленный множитель р).

Покажем, что в каждой из таких троек а, b, с один из «катетов» должен быть четным, а другой нечетным. Станем рассуждать «от противного». Если оба «катета» а и b четны, то четным будет число а² + b², а значит, и «гипотенуза». Это, однако, противоречит тому, что числа а, b, с не имеют общих множителей, так как три четных числа имеют общий множитель 2. Таким образом, хоть один из «катетов» а, b нечетен.

Остается еще одна возможность: оба «катета» нечетные, а «гипотенуза» четная. Нетрудно доказать, что этого не может быть. В самом деле: если «катеты» имеют вид

2х + 1 и 2y + 1,

то сумма их квадратов равна

4x² + 4х + 1 + 4у² + 4у + 1 = 4(х² + х + у² + у) + 2,

т. е. представляет собой число, которое при делении на 4 дает в остатке 2. Между тем квадрат всякого четного числа должен делиться на 4 без остатка. Значит, сумма квадратов двух нечетных чисел не может быть квадратом четного числа; иначе говоря, наши три числа — не пифагоровы.

Итак, из «катетов» а, b один четный, а другой нечетный. Поэтому число a² + b² нечетно, а значит, нечетна и «гипотенуза» с.

Предположим, для определенности, что нечетным является «катет» а, а четным b. Из равенства

а² + b² = с²

мы легко получаем:

а² = с² — b²= (с + b) (с — b).

Множители с + b и с — b, стоящие в правой части, взаимно просты. Действительно, если бы эти числа имели общий простой множитель, отличный от единицы, то на этот множитель делились бы и сумма

(c + b) + (c - b) = 2c,

и разность

(с + b) — (с — b) = 2b,

и произведение

(с + b) (с — b) = а²,

т. е. числа 2с, 2b и а имели бы общий множитель. Так как а нечетно, то этот множитель отличен от двойки, и потому этот же общий множитель имеют числа а, b, с, чего, однако, не может быть. Полученное противоречие показывает, что числа с + b и с — b взаимно просты.

Но если произведение взаимно простых чисел есть точный квадрат, то каждое из них является квадратом, т. е.

{	c + b = m²,
	c - b = n².

Решив эту систему, найдем:

с = (m² + n²) : 2, b = (m² - n²) : 2,

a² = (c + b) (c - b) = m²n², a = mn.

Итак, рассматриваемые пифагоровы числа имеют вид

а = mn, b = (m² - n²) : 2, с = (m² + n²) : 2,

где m и n — некоторые взаимно простые нечетные числа. Читатель легко может убедиться и в обратном: при любых нечетных m и n написанные формулы дают три пифагоровых числа а, b, с.

Вот несколько троек пифагоровых чисел, получаемых при различных тип:

при m = 3, n = 1 З² + 4² = 5²

при m = 5, n = 1 5² + 12² = 13²

при m = 7, n = 1 7² + 24² = 25²

при m = 9, n = 1 9² + 40² = 41²

при m = 11, n = 1 11² + 60² = 61²

при m = 13, n = 1 13² + 84² = 85²

при m = 5, n = 3 15²+ 8²= 17²

при m = 7, n = 3 21² + 20² = 29²

при m = 11, n = 3 33² + 56² = 65²

при m = 13, n = 3 39² + 80² = 89²

при m = 7, n = 5 35² + 12² = 37²

при m = 9, n = 5 45² + 28²= 53²

при m = 11, n = 5 55² + 48² = 73²

при m = 13, n = 5 65² + 72² = 97²

при m = 9, n = 7 63² + 16² = 65²

при m = 11, n = 7 77² + 36² = 85²

(Все остальные тройки пифагоровых чисел или имеют общие множители, или содержат числа, большие ста.)

Пифагоровы числа обладают вообще рядом любопытных особенностей, которые мы перечисляем далее без доказательств:

1) Один из «катетов» должен быть кратным трем.

2) Один из «катетов» должен быть кратным четырем.

3) Одно из пифагоровых чисел должно быть кратно пяти.

Читатель может удостовериться в наличии этих свойств, просматривая приведенные выше примеры групп пифагоровых чисел.

Ракеты

Сумма кубов трех целых чисел может быть кубом четвертого числа. Например, З³ + 4³ + 5³ = 6³.

Это означает, между прочим, что куб, ребро которого равно 6 см, равновелик сумме трех кубов, ребра которых равны 3 см, 4 см и 5 см (рис. 14), — соотношение, по преданию, весьма занимавшее Платона.

Попытаемся найти другие соотношения такого же рода, т. е. поставим перед собой такую задачу: найти решения уравнения х³ + у³ + z³= u³ Удобнее, однако,

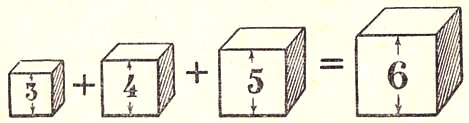
Рис. 14.

обозначить неизвестное u через — t. Тогда уравнение будет иметь более простой вид

х³ + у³ + z³ + t³ = 0.

Рассмотрим прием, позволяющий найти бесчисленное множество решений этого уравнения в целых (положительных и отрицательных) числах. Пусть а, b, с, d и α, β, γ, δ — две четверки чисел, удовлетворяющих уравнению. Прибавим к числам первой четверки числа второй четверки, умноженные на некоторое число k, и постараемся подобрать число k так, чтобы полученные числа

а + kα, b + kβ, с + kγ, d + kδ

также удовлетворяли нашему уравнению. Иначе говоря, подберем k таким образом, чтобы было выполнено равенство

(а + kα)³ + (b + kβ)³ + (с + kγ)³ + (d + kδ)³ = 0.

Раскрыв скобки и вспоминая, что четверки a, b, с, d и α, β, γ, δ удовлетворяют нашему уравнению, т. е. имеют место равенства

а³ + b³ + с³ + d³ = 0, α³ + β³ + γ³ + δ³ = 0,

мы получим:

3a²kα + 3ak²α² + 3b²kβ + 3bk²β² + 3c²kγ + 3ck²γ² + 3d²kδ + 3dk²δ² = 0

или

3k [(a²α + b²β + c²γ + d²δ) + k(aα² + bβ² + cγ² + dδ²)] = 0.

Произведение может обращаться в нуль только в том случае, когда обращается в нуль хотя бы один из его множителей. Приравнивая каждый из множителей нулю, мы получаем два значения для k. Первое значение, k = 0, нас не интересует: оно означает, что если к числам a, b, с, d ничего не прибавлять, то полученные числа удовлетворяют нашему уравнению. Поэтому мы возьмем лишь второе значение для k:

k = -	a²α + b²β + c²γ + d²δ
	aα² + bβ² + сγ² + dδ²

Итак, зная две четверки чисел, удовлетворяющих исходному уравнению, можно найти новую четверку: для этого нужно к числам первой четверки прибавить числа второй четверки, умноженные на k, где k имеет написанное выше значение.

Для того чтобы применить этот прием, надо знать две четверки чисел, удовлетворяющих исходному уравнению. Одну такую четверку (3, 4, 5, - 6) мы уже знаем. Где взять еще одну четверку? Выход из положения найти очень просто: в качестве второй четверки можно взять числа г, - r, s, - s, которые, очевидно, удовлетворяют исходному уравнению. Иначе говоря, положим:

а = 3, b = 4, с = 5, d = - 6,

α = г, β = - г, γ = s, δ = - s.

Тогда для k мы получим, как легко видеть, следующее значение:

k = -	-7r - 11s	=	7r + 11s
	7r² - s²		7r² - s²

а числа а + kα, b + kβ, с + kγ, d + kδ будут соответственно равны

28r² + 11rs — 3s², 21r² — 11rs — 4s²,

7r² — s² 7r² — s²

35r² + 7rs + 6s², — 42r² — 7rs — 5s².

7r² — s² 7r² — s²

Согласно сказанному выше эти четыре выражения удовлетворяют исходному уравнению

x³ + y³ + z³+ t³ = 0.

Так как все эти выражения имеют одинаковый зка» менатель, то его можно отбросить (т. е. числители этих дробей также удовлетворяют рассматриваемому уравнению). Итак, написанному уравнению удовле» творяют (при любых г и s) следующие числа:

x = 28r² + 11rs - 3s²,

у = 21г² - 11rs - 4s²,

z = 35r² + 7rs + 6s²,

t = - 42r² - 7rs - 5s².

в чем, конечно, можно убедиться и непосредственно, возведя эти выражения в куб и сложив. Придавая г и s различные целые значения, мы можем получить целый ряд целочисленных решений нашего уравнения. Если при этом получающиеся числа будут иметь общий множитель, то на него можно эти числа разделить. Например, при г = 1, s = 1 получаем для х, у, z, t следующие значения: 36, 6, 48, - 54, или, после сокращения на 6, значения 6, 1, 8, - 9. Таким образом,

6³ + 1³ + 8³ = 9³.

Вот еще ряд равенств того же типа (получающихся после сокращения на общий множитель):

при г = 1, s = 2 38³ + 73³= 17³ + 76³,

при г = 1, s = 3 17³ + 55³ = 24³ + 54³,

при г = 1, s = 5 4³ + 110³ = 67³ + 101³,

при г = 1, s = 4 8³ + 53³ = 29³ + 50³,

при г = 1, s = - 1 7³ + 14³+ 17³= 20³,

при г = 1, s = - 2 2³+ 16³= 9³ + 15³,

при г = 2, s = - 1 29³+ 34³ + 44³ = 53³.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Заметим, что если в исходной четверке, 3, 4, 5, - 6 или в одной из вновь полученных четверок поменять числа местами и применить тот же прием, то получим новую серию решений. Например, взяв четверку 3, 5, 4, - 6 (т. е. положив а = 3, b = 5, с = 4, d = - 6), мы получим для х, у, z, t значения:

_{х = 20r² + 10rs — 3s²,

у = 12г²— 10rs — 5s²,

z = 16г²+
8rs + 6s²,

t = - 24r²—
8rs — 4s².}

Отсюда при различных г и s получаем ряд новых соотношений:

при г = 1, s = 1 9³ + 10³ = 1³ + 12³,

при r = 1, s = 3 23³ + 94³ = 63³ + 84³,

при г = 1, s = 5 5³ + 163³ + 164³ = 206³,

при г = 1, s = 6 7³ + 54³ + 57³ = 70³,

при г = 2, s = 1 23³ + 97³ + 86³= 116³,

при г = 1, s = - 3 3³ + З6³ + 37³= 46³

и т. д.

Таким путем можно получить бесчисленное множество решений рассматриваемого уравнения.

Сто тысяч за доказательство теоремы

Одна задача из области неопределенных уравнений приобрела громкую известность, так как за правильное ее решение было завещано целое состояние: 100 000 немецких марок!

Задача состоит в том, чтобы доказать следующее положение, носящее название теоремы, или «великого предложения» Ферма:

Сумма одинаковых степеней двух целых чисел не может быть той же степенью какого-либо третьего целого числа. Исключение составляет лишь вторая степень, для которой это возможно.

Иначе говоря, надо доказать, что уравнение

хⁿ + уⁿ = zⁿ

неразрешимо в целых числах для n > 2.

Поясним сказанное. Мы видели, что уравнения

х² + y² = z²,

x³ + y³ + z³ = t³

имеют сколько угодно целочисленных решений. Но попробуйте подыскать три целых положительных числа, для которых было бы выполнено равенство x³ + y³ = z³; ваши поиски останутся тщетными.

Тот же неуспех ожидает вас и при подыскании примеров для четвертой, пятой, шестой и т. д. степеней. Это и утверждает «великое предложение Ферма».

Что же требуется от соискателей премии? Они должны доказать это положение для всех тех степеней, для которых оно верно. Дело в том, что теорема Ферма еще не доказана и висит, так сказать, в воздухе.

Прошло три столетия с тех пор, как она высказана, но математикам не удалось до сих пор найти ее доказательства.

Величайшие математики трудились над этой проблемой, однако в лучшем случае им удавалось доказать теорему лишь для того или иного отдельного показателя или для групп показателей, необходимо же найти общее доказательство для всякого целого показателя.

Замечательно, что неуловимое доказательство теоремы Ферма, по-видимому, однажды уже было найдено, но затем вновь утрачено. Автор теоремы, гениальный математик XVII в. Пьер Ферма, утверждал, что ее доказательство ему известно. Свое «великое предложение» он записал (как и ряд других теорем из теории чисел) в виде заметки на полях сочинения Диофанта, сопроводив его такой припиской:

«Я нашел поистине удивительное доказательство этого предложения, но здесь мало места, чтобы его привести».

Ни в бумагах великого математика, ни в его переписке, нигде вообще в другом месте следов этого доказательства найти не удалось.

Последователям Ферма пришлось идти самостоятельным путем.

Вот результаты этих усилий: Эйлер (1797) доказал теорему Ферма для третьей и четвертой степеней; для пятой степени ее доказал Лежандр (1823), для седьмой — Ламе и Лебег (1840). В 1849 г. Куммер доказал теорему для обширной группы степеней, и, между прочим, — для всех показателей, меньших ста. Эти последние работы далеко выходят за пределы той области математики, какая знакома была Ферма, и становится загадочным, как мог последний разыскать общее доказательство своего «великого предложения». Впрочем, возможно, он ошибался.

Интересующимся историей и современным состоянием задачи Ферма можно рекомендовать брошюру А. Я. Хинчина «Великая теорема Ферма». Написанная специалистом, брошюра эта предполагает у читателя лишь элементарные знания из математики.